在平面直角坐标系中求几何图形的面积VIP免费

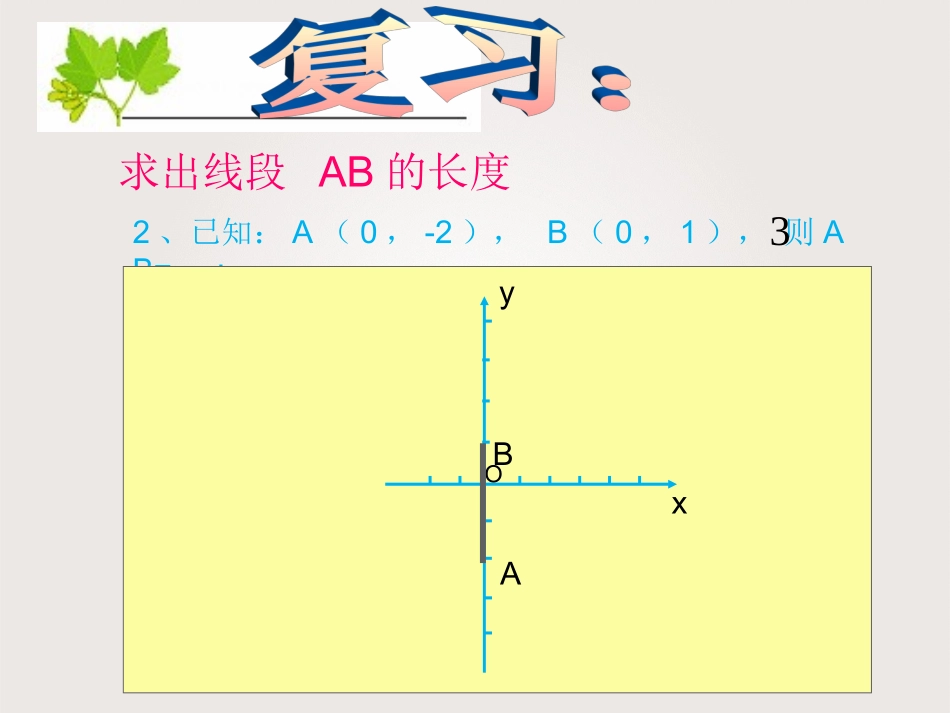
ABCDYXO1、P(-4、3)到x轴、y轴的距离分别为3、4yxO-5-4-3-2-154321(-4,3)P｜y｜到y轴的距离为点P(x、y)到x轴的距离为｜x｜2、已知：A（0，-2），B（0，1），则AB=;2、已知：A（5/2，0），B（-1/2，0），则AB=;3、已知：A（1，2），B（1，5），则AB=;4、已知：A（2，3），B（-5，3），则AB=;求出线段AB的长度xOyAB33、已知：A,B,则AB=;求出线段AB的长度xOyAB3)0,25()0,21(4、已知：A（2，2），B（2，5），则AB=;求出线段AB的长度xOyAB35、已知A（2，3），B（-5，3），则AB=;求出线段AB的长度OyxAB7A(x1，a)、B(x2，a)AB=A(x1a)B(x2，a)A(b，y1)B(b，y2)ooxxyyyA(b，y1)、B(b，y2)AB=|x1-x2||y1-y2|()例1;如图已知点A(-3，-2)B(0，3)C(-3，2)．求△ABC的面积．一、求三角形的面积有一边在坐标轴上或平行于坐标轴的三角形的面积解；作BD⊥CA交直线AC于点DSABC△=BD·AC=X3X4=621211.如图△AOB的面积是。6B(3,0)31425-2-4-1-3o12345-4-3-2-1xy•••A(0,4)2.如图所示，△ABC的面积是。C(3,0)B(-2,0)31425-2-4-1-3o12345-4-3-2-1xy•••A(0,5)12.5B(5,0)3.如图所示，△ABC的面积是。31425-2-4-1-3o12345-4-3-2-1xy•C(3,-4)HA(-1,0)••124.如图所示，△ABC的面积是。31425-2-4-1-3o12345-4-3-2-1xyH7.5•C(0,-2)A(-3,-1)••B(0,3)5.已知A（3,5）B(1,2）C（5,2）则△ABC的面积。1-2-1342512345-2-1xyo6•••B(1,2)A(3,5)C(5,2)H6.已知：A（-3,-2），B（-1,3），C（3,3），则△ABC的面积是。o31425-2-4-1-312345-4-3-2-1xyA(-3,-2)•••C(3,3)B(-1,3)10H7.已知：A（4,2）B(-2,4）C（-2,-1）则△ABC的面积是。1-2-1342512345-2-1xyo•A(4,2)••C(-2,-1)15HB(-2,4)选取在坐标轴上的边作为三角形的底。选取平行于坐标轴的边作为三角形的底。•A(5,2)1-2-1342512345-2-1xyo•B(3,4)•8.如图所示，求△OAB的面积。P②无边在坐标轴上或平行于坐标轴•A(5,2)1-2-1342512345-2-1xyo•B(3,4)•NMS=S梯形OAMN–S1–S2s1s28.如图，求△OAB的面积。解过B作MNy⊥轴过A作AMMN⊥交MN于点M.S=S梯形OAMN–S1–S2=(AM+ON)MN–BNON–AMBM=(2+4)×5–×3×4–×2×2=7212121212121•A(5,2)1-2-1342512345-2-1xyo•B(3,4)•MS=S梯形OPMB–S1–S2Ps1s28.如图所示，求△OAB的面积。•A(5,2)1-2-1342512345-2-1xyo•B(3,4)•MS=S△BOM+S梯形BMPA–SAOP△P8.如图所示，求△OAB的面积。•A(5,2)1-2-1342512345-2-1xyo•B(3,4)•NMS=S长方形OPMN–S1–S2–S3Ps1s2s38.如图所示，求△OAB的面积。•A(5,2)1-2-1342512345-2-1xyo•B(3,4)•8.如图所示，求△OAB的面积。P返回皮克公式格点图形的面积=周边经过的格点数一半+内部包含的格点数-1解；由皮克公式得S△AOB=解;S△AOB==70034520076421605234020025430)025430()052340(21求三角形的面积常常通过转化长方形、直角梯形、直角三角形的面积来计算。做一做已知;如图A(3,-1).B(1,3).C(2,-3).求出△ABC的面积ShugeHenggeGebu9.如图所示，则四边形AOBC的面积是。hengbuBuchangZuosyousYanchangxigeShsXias二、求四边形AOBC的面积•B(5,0)1-2-1342512345-2-1xyo••A(0,2)C(3,4)•MNs2S=S长方形NOMC+S2–S19.如图所示，则四边形AOBC的面积是。s113•B(5,0)1-2-1342512345-2-1xyo••A(0,2)C(3,4)•Ns1S=S梯形NOBC–S19.如图所示，则四边形AOBC的面积是。13•B(5,0)1-2-1342512345-2-1xyo••A(0,2)C(3,4)•Hs1s2S=S1+S29.如图所示，则四边形AOBC的面积是。13•B(5,0)1-2-1342512345-2-1xyo••A(0,2)C(3,4)•NMs1s2S=S长方形NOBM–S1–S29.如图所示，则四边形AOBC的面积是。13•B(5,0)1-2-1342512345-2-1xyo••A(0,2)C(3,4)•s1s2S=S1+S29.如图所示，则四边形AOBC的面积是。13•B(5,0)1-2-1342512345-2-1xyo••A(0,2)C(3,4)•Hs1s2s3S=S1+S2+S39.如图所示，则四边形AOBC的面积是。13求四边形的面积通过转化长方形、直角梯形、直角三角形的面积来计算。思考；若A(a,a)且AB⊥AC如何求四边形ABOC的面积1、点P(x、y)到x轴的距离为｜y｜、到y轴的距离为｜x｜点到轴距横标纵距，纵标横距绝对值2、A(x1，a)...