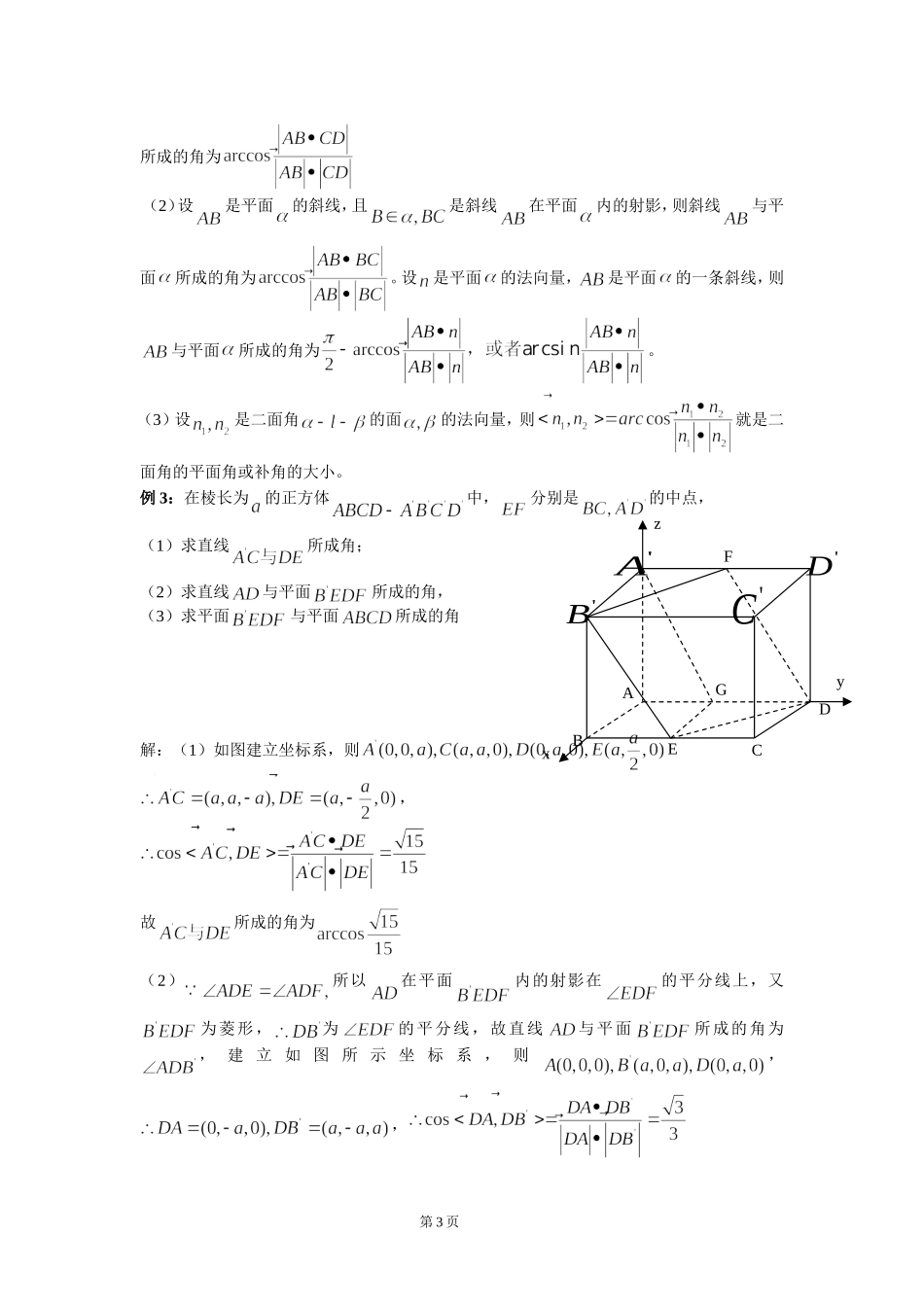
zABCDMNxyzzzz立体几何中几类典型问题的向量解法空间向量的引入为求立体几何的空间角和距离问题、证线面平行与垂直以及解决立体几何的探索性试题提供了简便、快速的解法。它的实用性是其它方法无法比拟的,因此应加强运用向量方法解决几何问题的意识,提高使用向量的熟练程度和自觉性,注意培养向量的代数运算推理能力,掌握向量的基本知识和技能,充分利用向量知识解决图形中的角和距离、平行与垂直问题。一、利用向量知识求点到点,点到线,点到面,线到线,线到面,面到面的距离(1)求点到平面的距离除了根据定义和等积变换外还可运用平面的法向量求得,方法是:求出平面的一个法向量的坐标,再求出已知点与平面内任一点构成的向量的坐标,那么到平面的距离(2)求两点之间距离,可转化求向量的模。(3)求点到直线的距离,可在上取一点,令或的最小值求得参数,以确定的位置,则为点到直线的距离。还可以在上任取一点先求,再转化为,则为点到直线的距离。(4)求两条异面直线之间距离,可设与公垂线段平行的向量,分别是上的任意两点,则之间距离例1:正方体的棱长为1,求异面直线与间的距离解:如图建立坐标系,则,设是直线与的公垂线,且则第1页ABCDxyz1A1B1C1D,例2:如图,在长方体中,求平面与平面的距离。解:,同理又,建立直角坐标系,,,设为平面的法向量,则由,不妨设,再选一条斜线段(端点分别在两个平面内),求斜线段对应的向量在法向量上的射影向量的模即可。点评:若是平面的法向量,是平面的一条斜线段,且,则点到平面的距离,平行平面之间的距离转化为点到平面的距离,变为斜线在法向量上的射影向量的模。二、利用向量知识求线线角,线面角,二面角的大小。(1)设是两条异面直线,是上的任意两点,是直线上的任意两点,则第2页所成的角为(2)设是平面的斜线,且是斜线在平面内的射影,则斜线与平面所成的角为。设是平面的法向量,是平面的一条斜线,则与平面所成的角为。(3)设是二面角的面的法向量,则就是二面角的平面角或补角的大小。例3:在棱长为的正方体中,分别是的中点,(1)求直线所成角;(2)求直线与平面所成的角,(3)求平面与平面所成的角解:(1)如图建立坐标系,则,故所成的角为(2)所以在平面内的射影在的平分线上,又为菱形,为的平分线,故直线与平面所成的角为,建立如图所示坐标系,则,,第3页'DABCDEFG'A'B'CxyzSBACDzxy故与平面所成角为由所以平面的法向量为下面求平面的法向量,设,由,,,所以平面与平面所成的角例4:如图,在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥面ABCD,SA=AB=BC=1,.求面SCD与面SBA所成的二面角的正切值.解:如图建立直角坐标系,则,所以是平面的一个法向量。设平面的一个法向量由,令,平面与平面所成的二面角的正切值为点评:用向量知识求二面角的大小时,是将二面角的问题转化为两平面的法向量的夹角问题,(1)当法向量的方向分别指向二面角内侧与外侧时,二面角的大小等于法向量的夹角的大小。(2)当法向量的方向同时指向二面角的内侧或外侧时,二面角的大小等于法向量的夹角的补角。三、利用向量知识解决立体几何中的探索性问题。例5:如图,在四棱锥P—ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DC,E、F分别是AB、PB的中点.(Ⅰ)求证:EF⊥CD;第4页(Ⅱ)在平面PAD内是否存在一点G,使GF⊥平面PCB,并证明你的结论;(Ⅲ)求DB与平面DEF所成角的大小.2、解:以DA、DC、DP所在直线为x轴、y轴、z轴建立空间直角坐标系(如图),设AD=a,则D(0,0,0)、A(a,0,0)、B(a,a,0)、C(0,a,0)、、(Ⅰ)(Ⅱ)假设存在,(Ⅲ)设平面DEF的法向量为例6:如图,在直三棱柱中,(1)求证(2)在上是否存在点使得(3)在上是否存在点使得解:直三棱柱,两两垂直,以为坐标原点,第5页ADBCDDD直线分别为轴轴,轴,建立空间直角坐标系,则,(1),(2)假设在上存在点,使得,则其中,则,于是由于,且所以得,所以在上存在点使得,且这时点与点重合。(3)假设在上存在点使得,则其中则,又由于,,所以存在实数成立,所以,所以在上存在点使得,且使的中点。练习1、如图5,在棱...