高中数学 理空间向量的应用同步练习 苏教版VIP免费

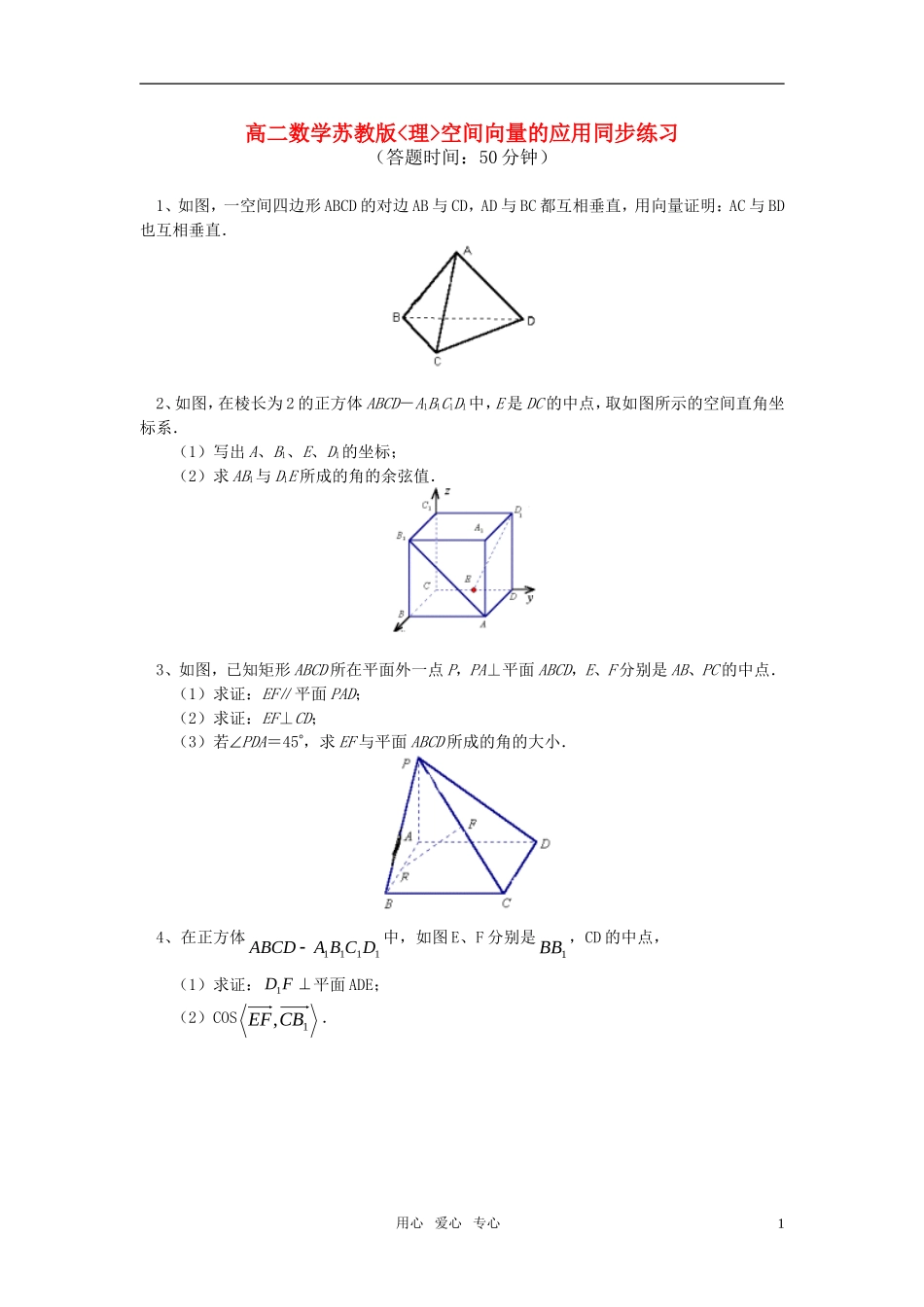
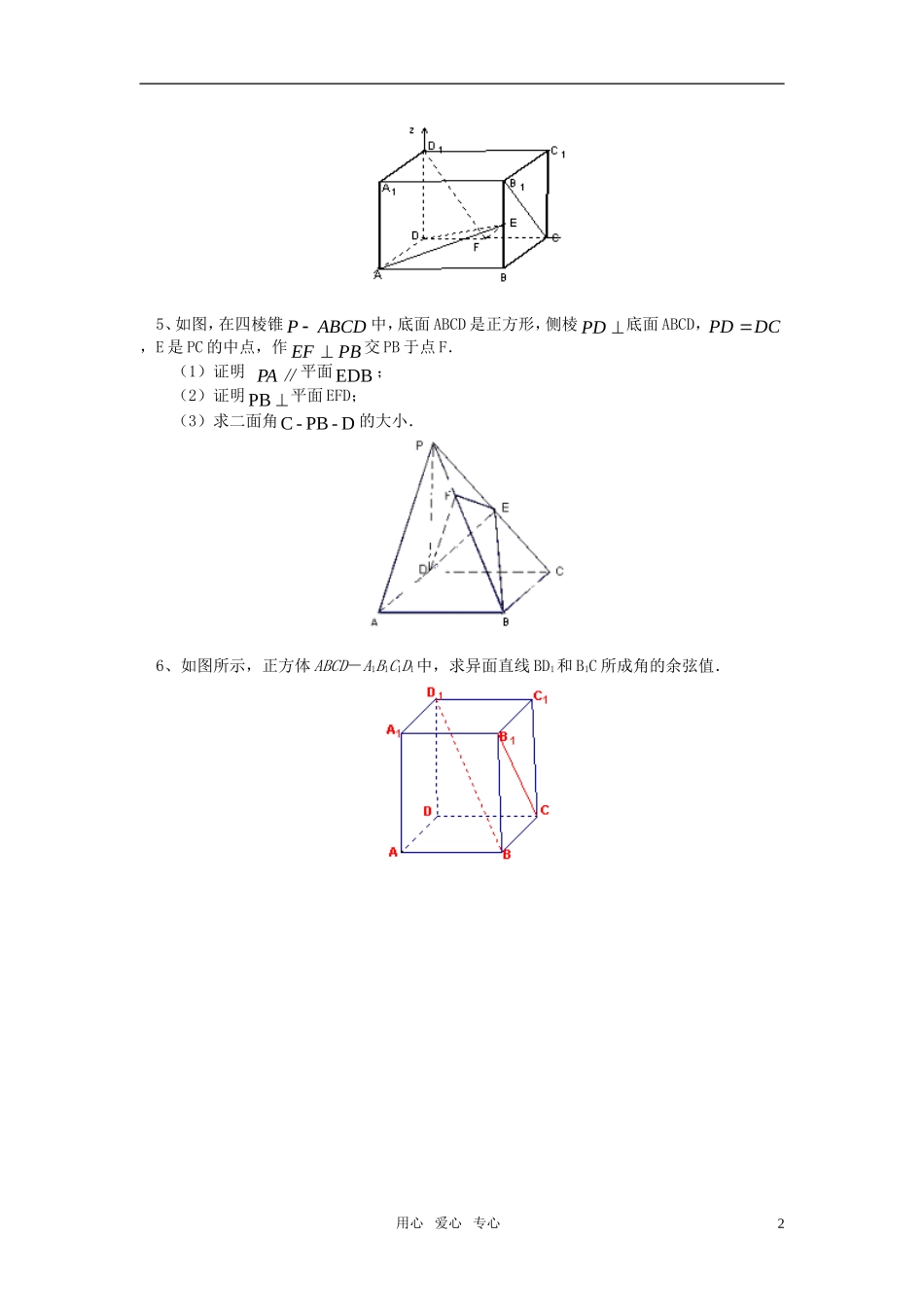
高二数学苏教版<理>空间向量的应用同步练习（答题时间：50分钟）1、如图，一空间四边形ABCD的对边AB与CD，AD与BC都互相垂直，用向量证明：AC与BD也互相垂直．2、如图，在棱长为2的正方体ABCD－A1B1C1D1中，E是DC的中点，取如图所示的空间直角坐标系．（1）写出A、B1、E、D1的坐标；（2）求AB1与D1E所成的角的余弦值．3、如图，已知矩形ABCD所在平面外一点P，PA⊥平面ABCD，E、F分别是AB、PC的中点．（1）求证：EF∥平面PAD；（2）求证：EF⊥CD；（3）若PDA＝45，求EF与平面ABCD所成的角的大小．4、在正方体1111DCBAABCD中，如图E、F分别是1BB，CD的中点，（1）求证：FD1平面ADE；（2）COS1,CBEF．用心爱心专心15、如图，在四棱锥ABCDP中，底面ABCD是正方形，侧棱PD底面ABCD，DCPD，E是PC的中点，作PBEF交PB于点F．（1）证明∥PA平面EDB；（2）证明PB平面EFD；（3）求二面角D-PB-C的大小．6、如图所示，正方体ABCD－A1B1C1D1中，求异面直线BD1和B1C所成角的余弦值．用心爱心专心2【试题答案】1、证明：0,CDABCDAB又CACBAB，0)(CDCACB即CDCACDCB……①0,BCADBCAD又CACDAD，0)(BCCACD即BCCABCCD……②由①＋②得：0BCCACDCA即0BDCABDAC2、解：（1）A（2，2，0），B1（2，0，2），E（0，1，0），D1（0，2，2）（2） ＝（0，－2，2），＝（0，1，2）∴||＝2，||＝，·＝0－2＋4＝2，∴cos，＝＝＝∴AB1与ED1所成的角的余弦值为．3、证：如图，建立空间直角坐标系A－xyz设AB＝2a，BC＝2b，PA＝2c则：A（0，0，0），B（2a，0，0），C（2a，2b，0），D（0，2b，0），P（0，0，2c） E为AB的中点，F为PC的中点∴E（a，0，0），F（a，b，c）（1） ＝（0，b，c），＝（0，0，2c），＝（0，2b，0）∴＝（＋）∴与、共面又 E平面PAD∴EF∥平面PAD．（2） ＝（－2a，0，0）∴·＝（－2a，0，0）·（0，b，c）＝0∴CD⊥EF．（3）若PDA＝45，则有2b＝2c，即b＝c∴＝（0，b，b），＝（0，0，2b）∴cos，＝＝∴，＝45 ⊥平面AC，∴是平面AC的法向量∴EF与平面AC所成的角为：90－，＝45．4、解：建立如图所示的直角坐标系，（1）不妨设正方体的棱长为1，用心爱心专心3则D（0，0，0），A（1，0，0），1D（0，0，1），E（1，1，21），F（0，21，0），则FD1＝（0，21，－1），AD＝（1，0，0），AE＝（0，1，21），则DAFD1＝0，AEFD1＝0，DAFD1，AEFD1.FD1平面ADE.（2）1B（1，1，1），C（0，1，0），故1CB＝（1，0，1），EF＝（－1，－21，－21），1CBEF＝－1＋0－21＝－23，2341411EF，21CB，则cos2322323,111CBEFCBEFCBEF.150,1CBEF.5、解：如图所示建立空间直角坐标系，D为坐标原点，设.DCa（1）证明：连结AC，AC交BD于G.连结EG.依题意得(,0,0),(0,0,),(0,,)22aaAaPaE底面ABCD是正方形，G是此正方形的中心，故点G的坐标为(,,0)22aa且(,0,),(,0,).22aaPAaaEG�2PAEG�.这表明EGPA∥.而EG平面EDB且PA平面EDB，PA∥平面EDB．用心爱心专心4GABCDPyxzEF（2）证明：依题意得(,,0),(,,)BaaPBaaa�．又(0,,),22aaDE�故022022aaDEPBPBDE，由已知EFPB，且,EFDEE所以PB平面EFD.（3）解：设点F的坐标为000(,,),,xyzPFPB�则000(,,)(,,)xyzaaaa从而000,,(1).xayaza所以00011(,,)(,(),()).2222aaFExyzaaa�由条件EFPB知，0PBPE即22211()()0,22aaa解得13．点F的坐标为2(,,),333aaa且2(,,),(,,).366333aaaaaaFEFD�03233222aaaFDPB，即PBFD故EFD是二面角CPBD的平面角. 691892222aaaaFDPE且aaaaFDaaaaPE369499,66363692222222.16cos.2||||66.63aFEFDEFDFEFDaa��3EFD所以，二面角C—PB—D的大小为.36、分析一：利用11BDBABCBB�11BCBCBB�，以及数量积的定义，可求出cos＜11,BDBC�＞，从而得到...