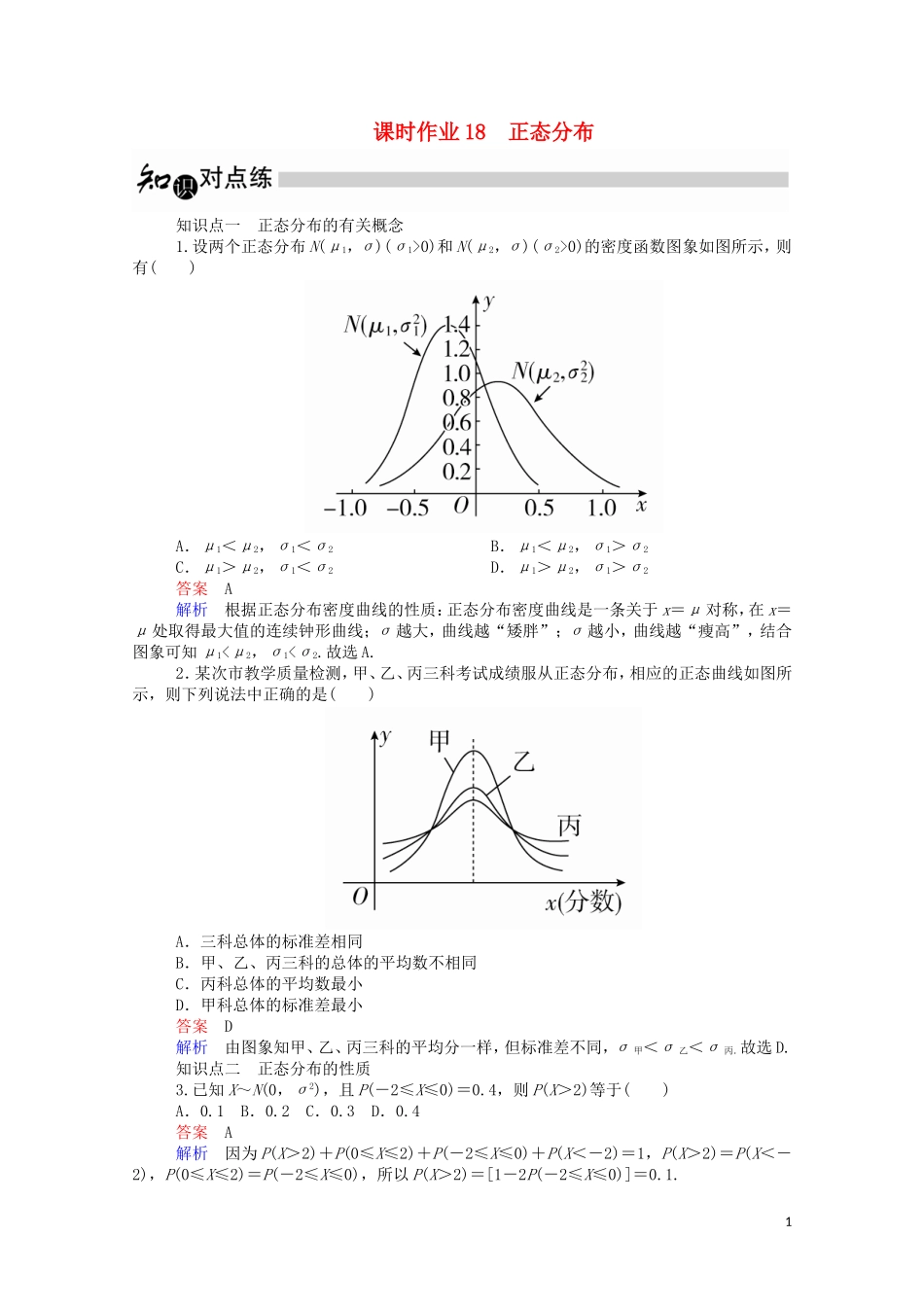
课时作业18正态分布知识点一正态分布的有关概念1.设两个正态分布N(μ1,σ)(σ1>0)和N(μ2,σ)(σ2>0)的密度函数图象如图所示,则有()A.μ1<μ2,σ1<σ2B.μ1<μ2,σ1>σ2C.μ1>μ2,σ1<σ2D.μ1>μ2,σ1>σ2答案A解析根据正态分布密度曲线的性质:正态分布密度曲线是一条关于x=μ对称,在x=μ处取得最大值的连续钟形曲线;σ越大,曲线越“矮胖”;σ越小,曲线越“瘦高”,结合图象可知μ1<μ2,σ1<σ2.故选A.2.某次市教学质量检测,甲、乙、丙三科考试成绩服从正态分布,相应的正态曲线如图所示,则下列说法中正确的是()A.三科总体的标准差相同B.甲、乙、丙三科的总体的平均数不相同C.丙科总体的平均数最小D.甲科总体的标准差最小答案D解析由图象知甲、乙、丙三科的平均分一样,但标准差不同,σ甲<σ乙<σ丙.故选D.知识点二正态分布的性质3.已知X~N(0,σ2),且P(-2≤X≤0)=0.4,则P(X>2)等于()A.0.1B.0.2C.0.3D.0.4答案A解析因为P(X>2)+P(0≤X≤2)+P(-2≤X≤0)+P(X<-2)=1,P(X>2)=P(X<-2),P(0≤X≤2)=P(-2≤X≤0),所以P(X>2)=[1-2P(-2≤X≤0)]=0.1.14.设随机变量X~N(1,22),则D等于()A.4B.2C.D.1答案D解析因为X~N(1,22),所以D(X)=4,所以D=D(X)=1.知识点三正态分布的应用5.已知一次考试共有60名同学参加,考生的成绩X~N(110,25).据此估计,大约应有57人的分数在区间()A.(90,110]内B.(95,125]内C.(100,120]内D.(105,115]内答案C解析=0.95,故可得大约应有57人的分数在区间(μ-2σ,μ+2σ)内,即在区间(110-2×5,110+2×5]内.6.某班同学共有48人,数学测验的分数服从正态分布,其平均分是80分,标准差是10分,则该班同学中成绩在70~90分的约有________人.答案33解析依题意,得μ=80,σ=10,所以P(70<ξ<90)=P(μ-σ<ξ<μ+σ)=0.6826,所以48×0.6826≈33(人).即该班约有33人的成绩在70~90分.一、选择题1.正态曲线关于y轴对称,当且仅当它所对应的正态总体的均值为()A.1B.-1C.0D.不确定答案C解析均值即为其对称轴,∴μ=0.2.如图所示的是当σ取三个不同值σ1,σ2,σ3的三种正态曲线N(0,σ2)的图象,那么σ1,σ2,σ3的大小关系是()A.σ1>1>σ2>σ3>0B.0<σ1<σ2<1<σ3C.σ1>σ2>1>σ3>0D.0<σ1<σ2=1<σ3答案D解析当μ=0,σ=1时,正态曲线f(x)=e在x=0处取最大值,故σ2=1.由正态曲线的性质,当μ一定时,曲线的形状由σ确定,σ越小,曲线越“瘦高”,反之越“矮胖”.故选D.3.已知随机变量X服从正态分布N(2,σ2),P(X<4)=0.84,则P(X≤0)等于()A.0.16B.0.32C.0.68D.0.842答案A解析由X~N(2,σ2),得正态曲线的对称轴为直线x=2,如图所示,可知P(X≤0)=P(X≥4)=1-P(X<4)=1-0.84=0.16,故选A.4.设随机变量ξ服从正态分布N(0,1),已知P(ξ<-1.96)=0.025,则P(|ξ|<1.96)=()A.0.025B.0.050C.0.950D.0.975答案C解析ξ服从正态分布N(0,1),则P(ξ<1.96)=1-P(ξ≤-1.96),从而P(|ξ|<1.96)=P(-1.96<ξ<1.96)=P(ξ<1.96)-P(ξ≤-1.96)=1-2P(ξ≤-1.96)=1-2×0.025=0.950.5.一批电阻的电阻值X(Ω)服从正态分布N(1000,52),现从甲、乙两箱出厂成品中各随机抽取一个电阻,测得电阻值分别为1011Ω和982Ω,可以认为()A.甲、乙两箱电阻均可出厂B.甲、乙两箱电阻均不可出厂C.甲箱电阻可出厂,乙箱电阻不可出厂D.甲箱电阻不可出厂,乙箱电阻可出厂答案C解析 X~N(1000,52),∴μ=1000,σ=5,∴μ-3σ=1000-3×5=985,μ+3σ=1000+3×5=1015. 1011∈(985,1015),982∉(985,1015),∴甲箱电阻可出厂,乙箱电阻不可出厂.二、填空题6.设ξ~N(1,4),那么P(3<ξ<5)=________.答案0.1359解析因为ξ~N(1,4),所以μ=1,σ=2,P(3<ξ<5)=P(-3<ξ<-1),则P(3<ξ<5)=[P(-3<ξ<5)-P(-1≤ξ≤3)]=[P(1-4<ξ<1+4)-P(1-2≤ξ≤1+2)]=[P(μ-2σ<ξ<μ+2σ)-P(μ-σ≤ξ≤μ+σ)]=(0.9544-0.6826)=0.1359.7.若随机变量ξ~N(10,σ2),若ξ在(5,10)上的概率等于a,...