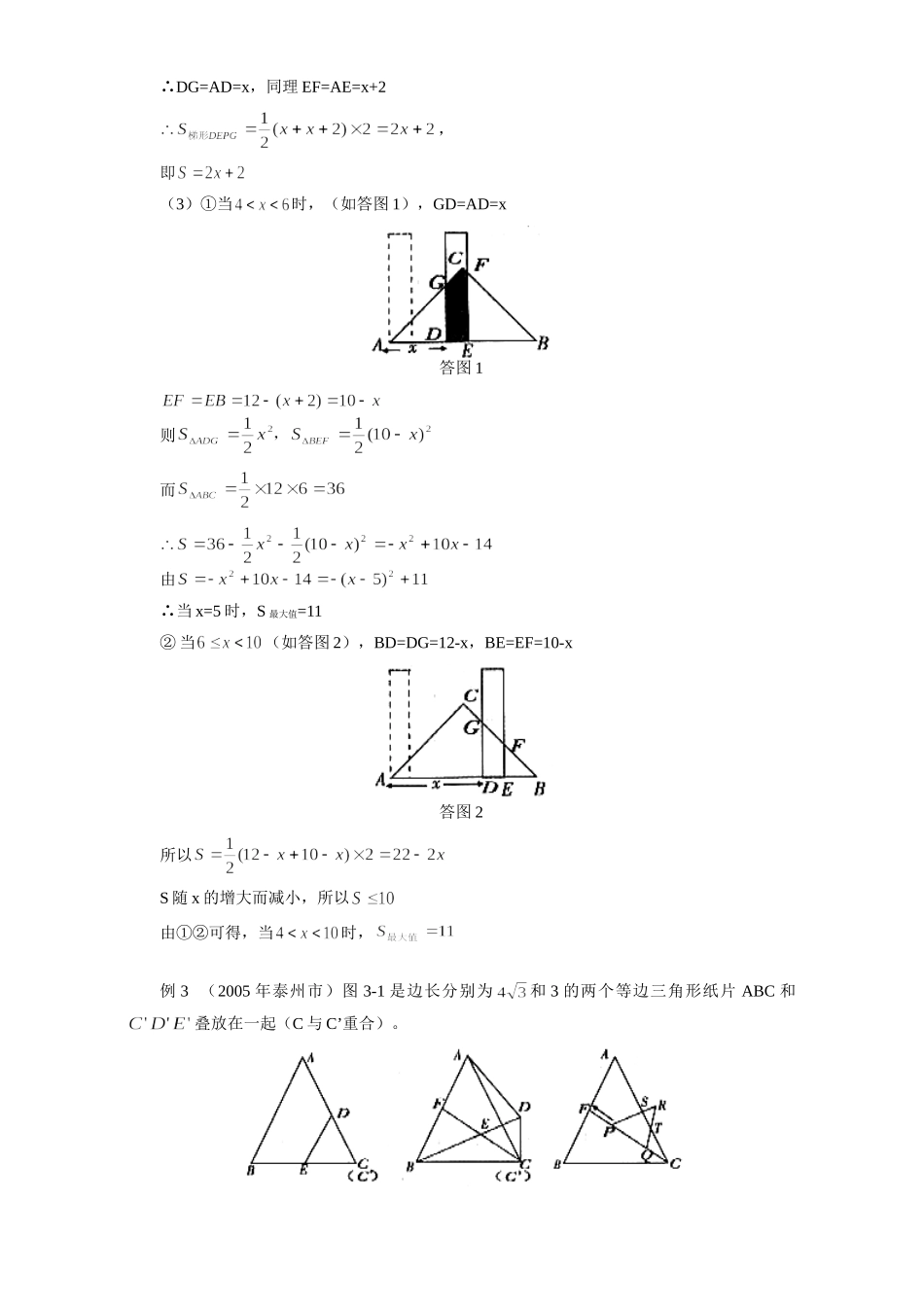
初三数学重叠图形的面积张宇石动态几何题是近几年来中考试题的热点题型,而其中求重叠图形的面积更是常作为压轴题,解此类题要化变量为常量,“动”中求“静”,这既展示了数学的创造过程,又考查了学生的应变能力和想像能力,现摘举数例与大家共赏。例1(2005年河南省)如图,Rt△PMN中,∠P=90°,PM=PN,MN=8cm,矩形ABCD的长和宽分别为8cm和2cm,C点和M点重合,BC和MN在一条直线上,令Rt△PMN不动,矩形ABCD沿MN所在直线向右以每秒1cm的速度移动(如图),直到C点与N点重合为止,设移动x秒后,矩形ABCD与△PMN重叠部分的面积为,求y与x之间的函数关系式。分析:首先分清矩形ABCD在运动过程中与Rt△PMN重叠部分的形状,这是解题r关键,然后将重叠图形中涉及到的线段用含x的代数式表示,最后再转化成函数关系式,这是解此类题的基本思路。当矩形ABCD从开始运动到停止,和Rt△PMN重叠部分的形状共有三种情况。首先当时,重叠部分是等腰直角三角形,然后在的过程中,重叠部分是直角梯形,最后当时,重叠部分是一个五边形,搞清这几个变化过程是解本题的关键。解:在中, PM=PN,∠P=90°延长AD分别交PM、PN于点G、H,过G作GF⊥MN于F,过H作HT⊥MN于T。 DC=2cm,∴MF=GF=2cm,TN=HT=2cm∴MN=8cm,∴MT=6cm因此,矩形ABCD以每秒1cm的速度由开始向右移动到停止,和Rt△PMN重叠部分的形状可分为下列三种情况:图1-1图1-2(1)当C点由M点运动到F点的过程中()如图1-1所示,设CD与PM交于点E,则重叠部分图形是,且(2)当C点由F点运动到T点的过程中(),如图1-2所示,重叠部分图形是直角梯形MCDG,,且DC=2(3)当C点由T点运动到N点的过程中(),如图1-3所示,设CD与PN交于点Q,则重叠部分图形是五边形MCQHG。图1-3且例2(2005年徐州市)有一根直尺的短边长2cm,长边长10cm,还有一块锐角为45°的直角三角形纸板,它的斜边长12cm,如图2-1,将直尺的短边DE放置与直角三角形纸板的斜边AB重合,且点D与点A重合,将直尺沿AB方向平移(如图2-2),设平移的长度为xcm(0≤x≤10),直尺和三角形纸板的重叠部分(图中阴影部分)的面积为。图2-1图2-2(1)当x=0(如图2-1),S=________,当x=10时,S=_________。(2)当时,(如图2-2),求S关于x的函数关系式;(3)当时,求S关于x的函数关系式,并求出S的最大值。分析:(1)当x=0和x=10这两个特殊值时,重叠部分是两个等腰直角三角形;(2)当时,重叠部分是直角梯形(3)由函数最值问题,首先想到的是二次函数的最值。解:(1)2,2(2)在Rt△ADG中,∠A=45°∴DG=AD=x,同理EF=AE=x+2,即(3)①当时,(如答图1),GD=AD=x答图1则而由∴当x=5时,S最大值=11②当(如答图2),BD=DG=12-x,BE=EF=10-x答图2所以S随x的增大而减小,所以由①②可得,当时,例3(2005年泰州市)图3-1是边长分别为和3的两个等边三角形纸片ABC和叠放在一起(C与C’重合)。图3-1图3-2图3-3(1)操作:固定△ABC,将△C’D’E’绕C顺时针旋转30°得到△CDE。连结AD、BE、CD的延长线交AB于F(图3-2);探究:在图3-2中,线段BE与AD之间有怎样的大小关系?试证明你的结论。(2)操作:将图3-2中的CDE,在线段CF上沿着CF方向以每秒1个单位的速度平移,平移后的△CDE设为△PQR(图3-3);探究:设△PQR移动的时间为x秒,△PQR与△AFC重叠部分的面积为y,求y与x之间的函数解析式,并写出函数自变量x的取值范围。分析:(1)只需证△BCE和△ACD全等即可,也可用旋转方法证明。(2)△PQR在运动过程中,和△ACF重叠部分始终是四边形PQTS,其面积等于△PQR与△RTS的面积差。解:(1)BE=AD证明: (也可用旋转方法证明BE=AD)(2)如图3-4,在△CQT中,图3-4例4(2005年南京市)如图4,形如量角器的半圆O的直径DE=12cm,形如三角板的△ABC中,∠ACB=90°,∠ABC=30°,BC=12cm,半圆O以2cm/s的速度从左向右运动,在运动过程中,点D、E始终在直线BC上,设运动时间为t(s),当t=Os时,半圆O在△ABC的左侧,OC=8cm,(1)当t为何值时,△ABC的一边所在的直线与半圆O所在的圆相切?(2)当△ABC的一边所在的直线与半圆O所在的圆相切时,如果半圆O与直径DE围成的区域与...