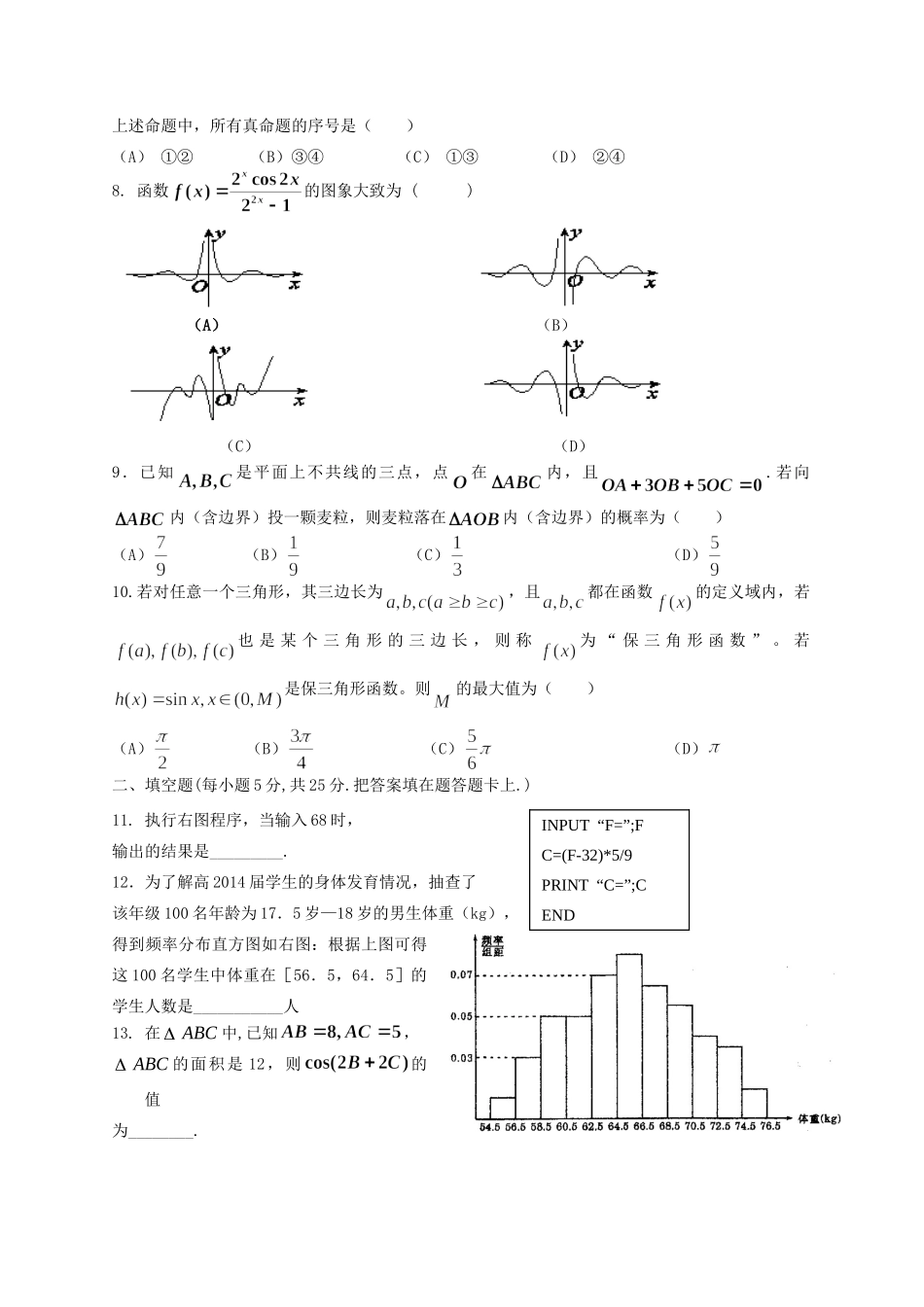
正(主)视图俯视图侧(左)视图414111成都七中2014级考试数学试卷(文科)一、选择题(每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合要求的.)1.已知集合,,则的元素个数为()(A)(B)(C)(D)2.已知命题命题,则()(A)命题是假命题(B)命题是真命题(C)命题是假命题(D)命题是真命题3.已知为虚数单位,则复数与的积是实数的充要条件是()(A)(B)(C)(D)4.某四棱锥的三视图如图所示,记A为此棱锥所有棱的长度的集合,则()(A)2AÎ,且4AÎ(B)2AÎ,且4AÎ(C)2AÎ,且25AÎ(D)2AÎ,且17AÎ5.国色天香的观览车的主架示意图如图所示,其中O为轮轴的中心,距地面32m(即OM长),巨轮的半径为30m,AM2BPm,巨轮逆时针旋转且每12分钟转动一圈.若点M为吊舱P的初始位置,经过t分钟,该吊舱P距离地面的高度为()htm,则()ht=()(A).ππ30sin()30122t(B).ππ30sin()3062t(C).ππ30sin()3262t(D).ππ30sin()62t6.已知抛物线与椭圆交于两点,点为抛物线与椭圆的公共焦点,且共线则该椭圆的离心率为()(A)(B)(C)(D)7.设为空间的两条不同的直线,为空间的两个不同的平面,给出下列命题:①若∥,∥,则∥;②若,则∥;③若∥,∥,则∥;④若,则∥.hPAOMB上述命题中,所有真命题的序号是()(A)①②(B)③④(C)①③(D)②④8.函数的图象大致为()(A)(B)(C)(D)9.已知是平面上不共线的三点,点在内,且.若向内(含边界)投一颗麦粒,则麦粒落在内(含边界)的概率为()(A)(B)(C)(D)10.若对任意一个三角形,其三边长为,且都在函数的定义域内,若也是某个三角形的三边长,则称为“保三角形函数”。若是保三角形函数。则的最大值为()(A)(B)(C)(D)二、填空题(每小题5分,共25分.把答案填在题答题卡上.)11.执行右图程序,当输入68时,输出的结果是_________.12.为了解高2014届学生的身体发育情况,抽查了该年级100名年龄为17.5岁—18岁的男生体重(kg),得到频率分布直方图如右图:根据上图可得这100名学生中体重在[56.5,64.5]的学生人数是___________人13.在ABC中,已知,ABC的面积是12,则的值为________.INPUT“F=”;FC=(F-32)*5/9PRINT“C=”;CEND14.已知椭圆,左,右焦点分别为,过的直线交椭圆于两点,若的最大值是,则的值是_______.15.关于三次函数,以下说法正确的有_________。①可能无零点②一定是中心对称图形,且对称中心一定在的图象上③至多有2个极值点④当有两个不同的极值点,且,,则方程的不同实根个数为:个或个.三、解答题(本大题共6小题.共75分.题每题12分,20题13分,21题14分,解答应写出文字说明、证明过程或演算步骤.)16.已知数列{}na,其前n项和为nS,点(,)nnS在抛物线23122yxx上;各项都为正数的等比数列{}nb满足13511,1632bbb.(Ⅰ)求数列{}na,{}nb的通项公式;(Ⅱ)记nnnCab,求数列{}nC的前项和nT.17.在△中,角、、所对的边分别是、、,且(其中为△的面积).(Ⅰ)求;(Ⅱ)若,△的面积为3,求.ABCPH18.某日用品按行业质量标准分成五个等级,等级系数依次为1,2,3,4,5.现从一批该日用品中随机抽取20件,对其等级系数进行统计分析,得到频率分布表如下:(1)若所抽取的20件日用品中,等级系数为4的恰有3件,等级系数为5的恰有2件,求,,的值;(Ⅱ)在(1)的条件下,将等级系数为4的3件日用品记为,,,等级系数为5的2件日用品记为,,现从,,,,这5件日用品中任取两件(假定每件日用品被取出的可能性相同),写出所有可能的结果,并求这两件日用品的等级系数恰好相等的概率.19.如图,在三棱锥ABCP中,PA底面ABC,ACBC,H为PC的中点,2PAAC,1BC.(Ⅰ)求证:AH平面PBC;(Ⅱ)求经过点的球的表面积。12345频率0.20.4520.已知抛物线与轴交点为,动点在抛物线上滑动,且(1)求中点的轨迹方程;(2)点在上,关于轴对称,过点作切线,且与平行,点到的距离为,且,证明:为直角三角形21.设函数.(1)求的极大值;(2)求证:(3)当方程有唯一解时,方程也有唯一解,求正实数的值;成都七中2014级考试...