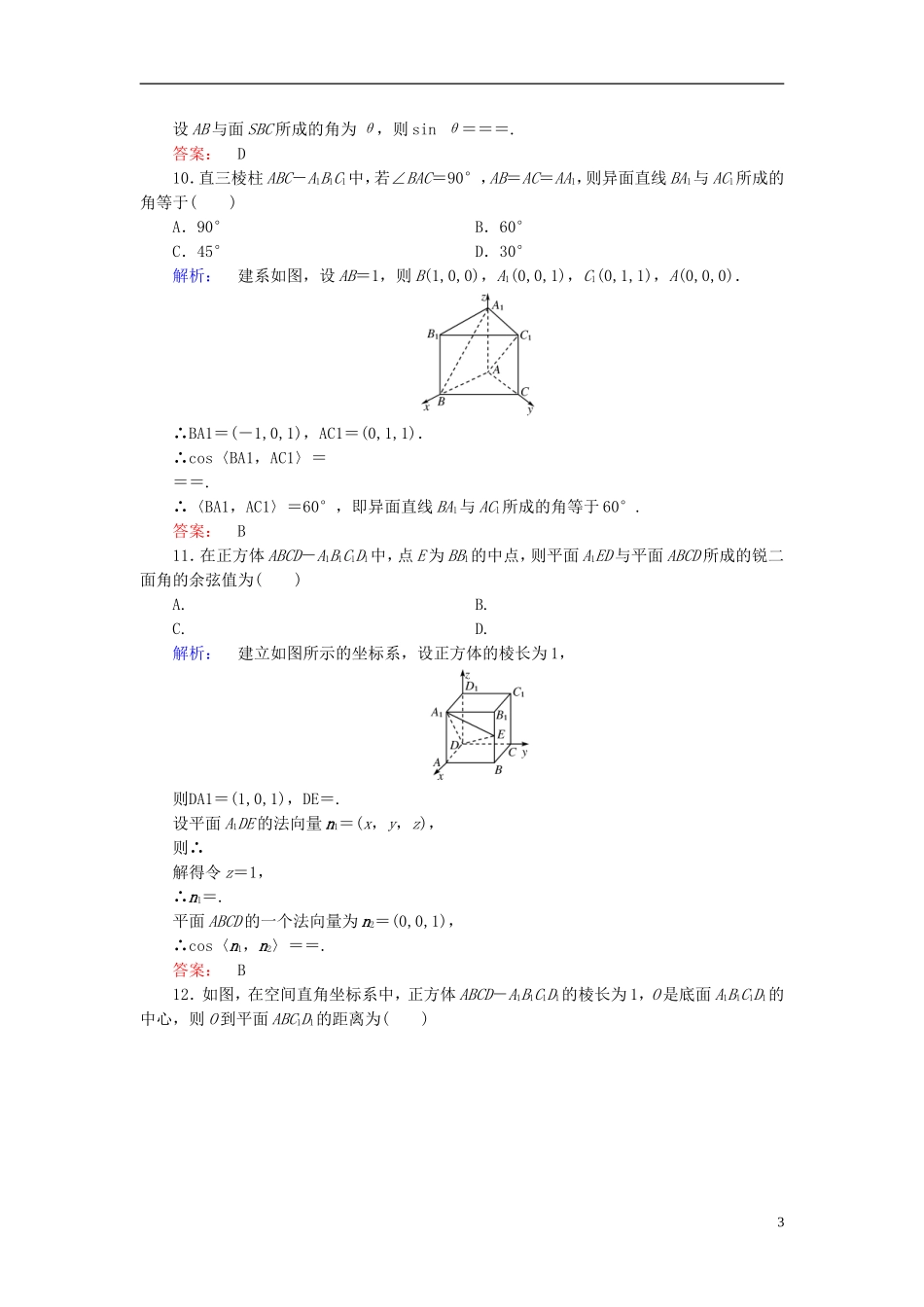
第三章空间向量与立体几何一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.若A,B,C,D为空间不同的四点,则下列各式为零向量的是()①AB+2BC+2CD+DC;②2AB+2BC+3CD+3DA+AC;③AB+CA+BD;④AB-CB+CD+AD.A.①②B.②③C.②④D.①④解析:①中,原式=AB+2BD+DC=AB+BD+BD+DC=AD+BC,不符合题意;②中,原式=2(AB+BC+CD+DA)+(AC+CD+DA)=0;③中,原式=CD,不符合题意;④中,原式=(AB-AD)+(CD-CB)=0.故选C.答案:C2.已知向量a=(2,4,5),b=(3,x,y)分别是直线l1,l2的方向向量,若l1∥l2,则()A.x=6,y=15B.x=3,y=C.x=3,y=15D.x=6,y=解析: l1∥l2,∴a∥b,则==,∴x=6,y=.答案:D3.在下列四个命题中,真命题为()A.已知三向量a,b,c,则空间任意一个向量p总可以唯一地写成p=xa+yb+zcB.若a,b,c三向量两两不共线,则空间任意一个向量p总可以写成p=xa+yb+zcC.若a,b,c不共面,则空间任意一个向量p总可以唯一地写成p=xa+yb+zcD.若a,b,c三向量两两不共线,则xa+yb+zc=0的充要条件是x=y=z=0解析:对于空间作为基底的三向量a,b,c必须要有限制,即不共面,故C正确.答案:C4.若两点A(x,5-x,2x-1),B(1,x+2,2-x),当|AB|取最小值时,x的值等于()A.19B.-C.D.解析:AB=(1-x,2x-3,-3x+3),则|AB|===.故当x=时,|AB|取最小值.答案:C5.已知A(2,-5,1),B(2,-2,4),C(1,-4,1),则AB与AC的夹角为()A.30°B.45°C.60°D.90°解析:AB=(0,3,3),AC=(-1,1,0),|AB|=3,|AC|=,AB·AC=3,∴cos〈AB,AC〉==,∴〈AB,AC〉=60°.1答案:C6.已知向量AM=,AN=,则平面AMN的一个法向量是()A.(-3,-2,4)B.(3,2,-4)C.(-3,-2,-4)D.(-3,2,-4)解析:设平面AMN的法向量n=(x,y,z),则即令z=4,则n=(3,-2,4),由于(-3,2,-4)=-(3,-2,4),可知选项D符合.答案:D7.已知空间三点A(0,2,3),B(-2,1,6),C(1,-1,5).若|a|=,且a分别与AB,AC垂直,则向量a为()A.(1,1,1)B.(-1,-1,-1)或(1,1,1)C.(-1,-1,-1)D.(1,-1,1)或(-1,1,-1)解析:设a=(x,y,z),AB=(-2,-1,3),AC=(1,-3,2),则解得a=(1,1,1)或(-1,-1,-1).答案:B8.已知空间四边形ABCD的每条边和对角线的长都等于a,点E,F分别是BC,AD的中点,则AE·AF的值为()A.a2B.a2C.a2D.a2解析:如下图,AE=(AB+AC),AF=AD,AE·AF=(AB·AD+AC·AD)=(a2cos60°+a2cos60°)=a2.答案:C9.已知三棱锥S-ABC中,底面ABC为边长等于2的等边三角形,SA垂直于底面ABC,SA=3,那么直线AB与平面SBC所成角的正弦值为()A.B.C.D.解析:建系如图,则S(0,0,3),A(0,0,0),B(,1,0),C(0,2,0).∴AB=(,1,0),SB=(,1,-3),SC=(0,2,-3).设面SBC的法向量为n=(x,y,z).则令y=3,则z=2,x=,∴n=(,3,2).2设AB与面SBC所成的角为θ,则sinθ===.答案:D10.直三棱柱ABC-A1B1C1中,若∠BAC=90°,AB=AC=AA1,则异面直线BA1与AC1所成的角等于()A.90°B.60°C.45°D.30°解析:建系如图,设AB=1,则B(1,0,0),A1(0,0,1),C1(0,1,1),A(0,0,0).∴BA1=(-1,0,1),AC1=(0,1,1).∴cos〈BA1,AC1〉===.∴〈BA1,AC1〉=60°,即异面直线BA1与AC1所成的角等于60°.答案:B11.在正方体ABCD-A1B1C1D1中,点E为BB1的中点,则平面A1ED与平面ABCD所成的锐二面角的余弦值为()A.B.C.D.解析:建立如图所示的坐标系,设正方体的棱长为1,则DA1=(1,0,1),DE=.设平面A1DE的法向量n1=(x,y,z),则∴解得令z=1,∴n1=.平面ABCD的一个法向量为n2=(0,0,1),∴cos〈n1,n2〉==.答案:B12.如图,在空间直角坐标系中,正方体ABCD-A1B1C1D1的棱长为1,O是底面A1B1C1D1的中心,则O到平面ABC1D1的距离为()3A.B.C.D.解析:连接A1D,则O,C1(0,1,1).易知平面ABC1D1的一个法向量n=DA1=(1,0,1),与之同向的单位向量为n0=,∴d=|C1O·n0|=.答案:B二、填空题(本大题共4小题,每小题4分,共16分...