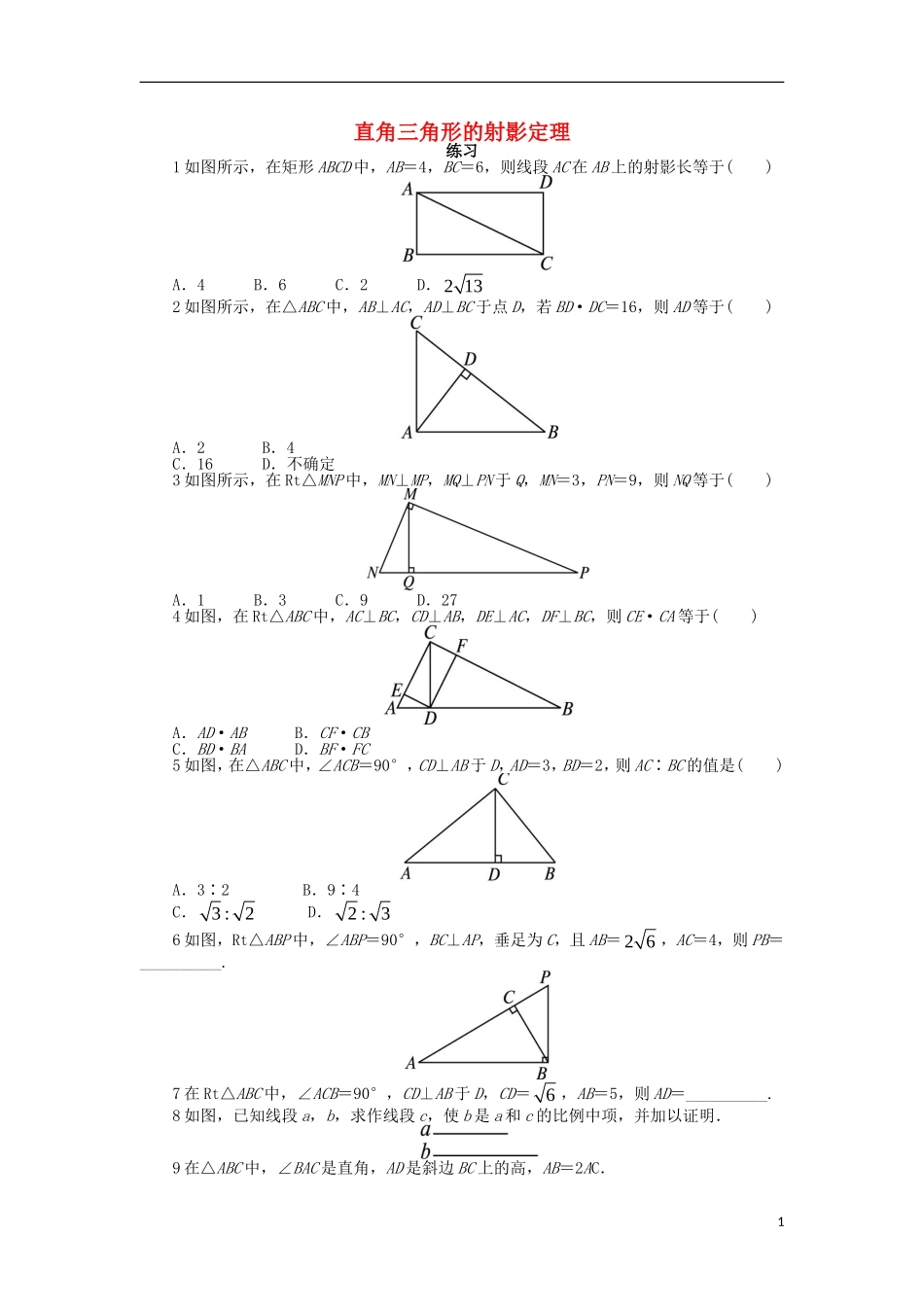
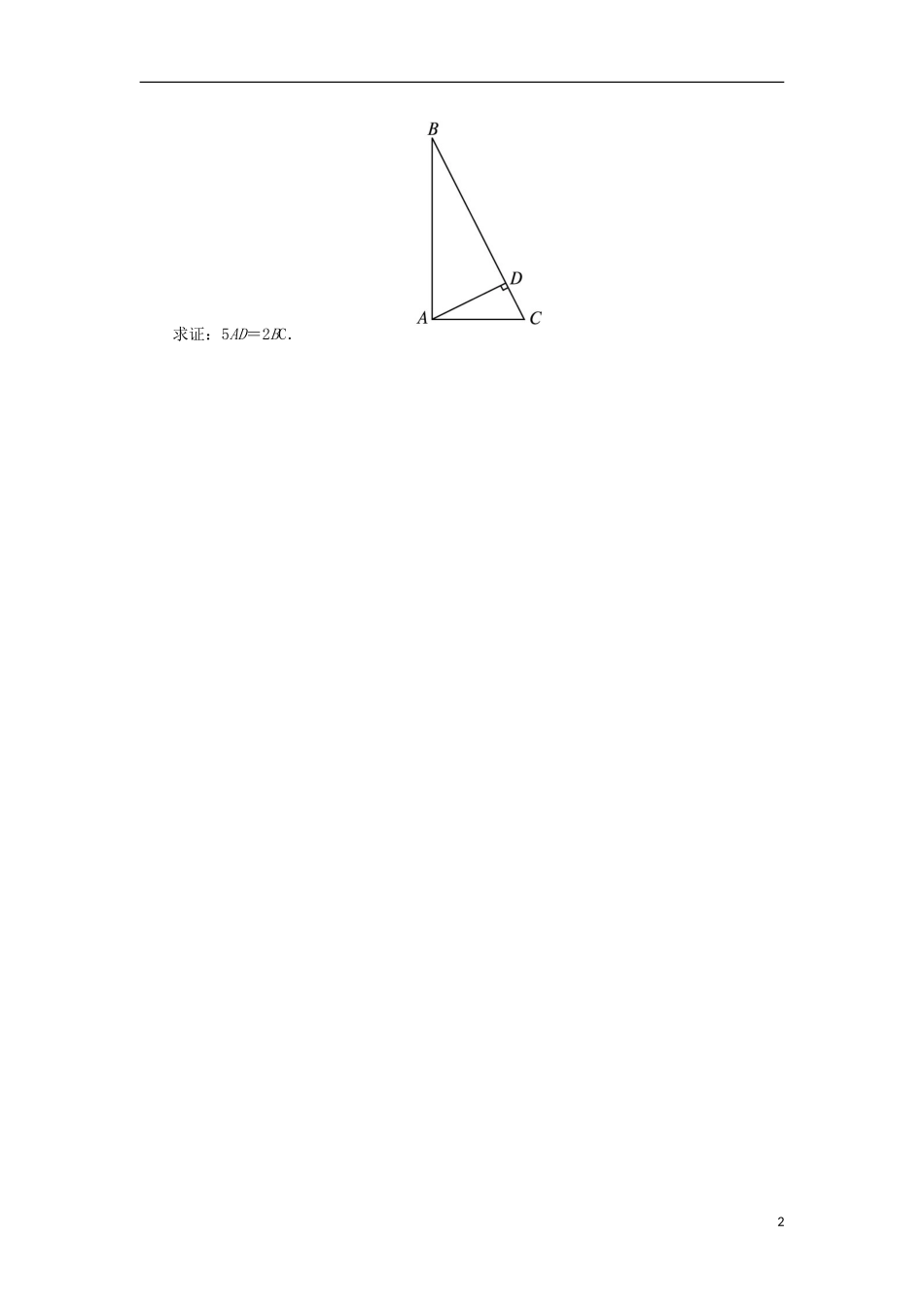
直角三角形的射影定理练习1如图所示,在矩形ABCD中,AB=4,BC=6,则线段AC在AB上的射影长等于()A.4B.6C.2D.2132如图所示,在△ABC中,AB⊥AC,AD⊥BC于点D,若BD·DC=16,则AD等于()A.2B.4C.16D.不确定3如图所示,在Rt△MNP中,MN⊥MP,MQ⊥PN于Q,MN=3,PN=9,则NQ等于()A.1B.3C.9D.274如图,在Rt△ABC中,AC⊥BC,CD⊥AB,DE⊥AC,DF⊥BC,则CE·CA等于()A.AD·ABB.CF·CBC.BD·BAD.BF·FC5如图,在△ABC中,∠ACB=90°,CD⊥AB于D,AD=3,BD=2,则AC∶BC的值是()A.3∶2B.9∶4C.3:2D.2:36如图,Rt△ABP中,∠ABP=90°,BC⊥AP,垂足为C,且AB=26,AC=4,则PB=__________.7在Rt△ABC中,∠ACB=90°,CD⊥AB于D,CD=6,AB=5,则AD=__________.8如图,已知线段a,b,求作线段c,使b是a和c的比例中项,并加以证明.9在△ABC中,∠BAC是直角,AD是斜边BC上的高,AB=2AC.1求证:5AD=2BC.2参考答案1答案:A∵BC⊥AB,∴AC在AB上的射影是AB.2答案:B由题意知,AD2=BD·DC=16,故AD=4.3答案:A∵MN2=NQ·NP,∴32=NQ×9.∴NQ=1.4答案:B∵CD⊥AB,DE⊥AC,∴CD2=CE·CA,同理可得CD2=CF·CB,∴CE·CA=CF·CB.5答案:C在Rt△ABC中,∠ACB=90°,CD⊥AB,由射影定理知,AC2=AD·AB,BC2=BD·AB.又∵AD=3,BD=2,∴AB=AD+BD=5,∴AC2=3×5=15,BC2=2×5=10.∴153102ACBC,即AC∶BC=3:2.6答案:23∵在Rt△ABP中,∠ABP=90°,BC⊥AP,∴AB2=AC·AP,即2(26)=4AP,解得AP=6.在Rt△ABP中,由勾股定理,得22226(26)23BPAPAB.7答案:2或3∵∠ACB=90°,CD⊥AB,∴CD2=AD·DB.∵CD=6,∴AD·DB=6.又AB=5,∴DB=5-AD.∴AD(5-AD)=6,解得AD=2或3.8答案:作法:如图所示.(1)作线段AB=a,过B作AB的垂线l,在l上取一点C,使BC=b;(2)连接AC,过C作AC的垂线l′,l′交AB的延长线于D,则线段BD为所求作线段c.证明:∵AC⊥CD,CB⊥AD,∴CB2=AB·BD.∴b2=ac,即线段c使得b是a和c的比例中项.9答案:证明:在Rt△ABC中,设AC=k,则AB=2AC=2k,∴225BCACABk,AC2=BC·CD=5k·CD=k2,则CD=55k.∵AD2=CD·BD,BD=BC-CD=455k,∴AD2=55k×455k,∴AD=255k.∴AD∶BC=25.即5AD=2BC.3