高二数学椭圆人教版知识精点VIP免费

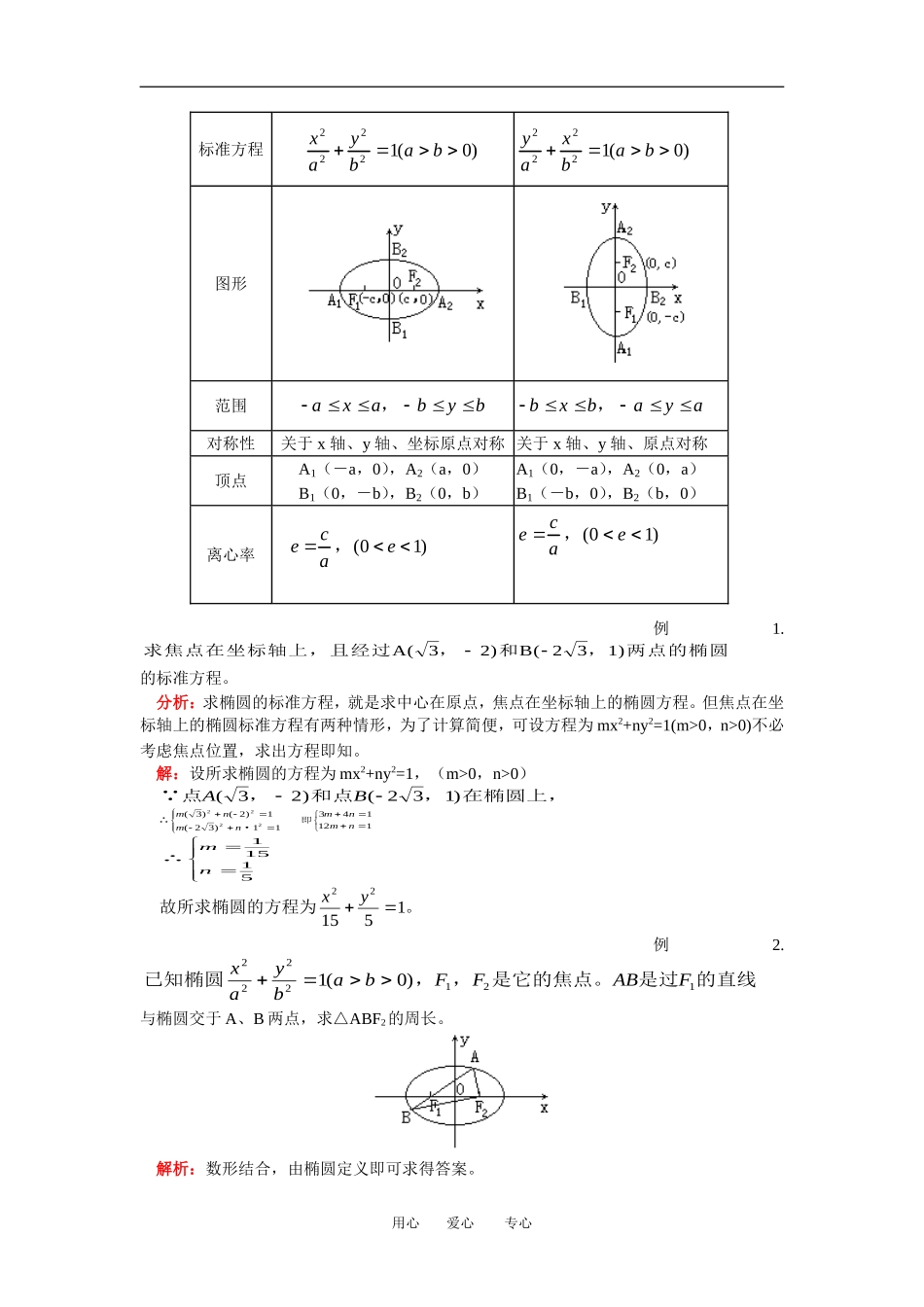
高二数学椭圆人教版【同步教育信息】一.本周教学内容：椭圆教学目标：1.掌握椭圆的定义。（第一定义和第二定义）。2.能根据条件熟练求出椭圆的标准方程；3.掌握椭圆的几何性质及标准方程中的a、b、c、e的几何意义，及a、b、c、e间的相互关系；4.能综合应用椭圆的有关知识解决最值问题及参数的取值范围；5.理解直线与椭圆的位置关系，会求椭圆截直线所得的弦长，会应用弦中点的性质求解问题。能力训练：进一步巩固求曲线方程的方法，提高运用坐标法的自觉性及解决几何问题的能力；进一步培养数形结合的能力；同时提高代数运算能力、综合分析问题解决问题的能力。二.重点、难点：重点：椭圆的定义、标准方程及几何性质的应用。难点：椭圆的定义、标准方程、几何性质在解题过程中的灵活运用。【典型例题】一.知识提要：1.椭圆的第一定义：平面内，与两个定点F1、F2的距离和等于常数（大于|F1F2|）的点的轨迹叫做椭圆。这两个定点叫做椭圆的焦点，两焦点的距离叫椭圆的焦距。2.椭圆的第二定义：平面内，动点与定点（，）的距离和它到定直线：的距离的MFc0lxac2比是常数的点的轨迹是椭圆。定点是椭圆的焦点，定直线叫做椭caacM()0圆的准线，常数叫椭圆的离心率。ca3.椭圆的标准方程及几何性质：用心爱心专心标准方程xaybab222210()yaxbab222210()图形范围axabyb，bxbaya，对称性关于x轴、y轴、坐标原点对称关于x轴、y轴、原点对称顶点A1（－a，0），A2（a，0）B1（0，－b），B2（0，b）A1（0，－a），A2（0，a）B1（－b，0），B2（b，0）离心率ecae，()01ecae，()01例1.求焦点在坐标轴上，且经过，和，两点的椭圆A(32)B(231)的标准方程。分析：求椭圆的标准方程，就是求中心在原点，焦点在坐标轴上的椭圆方程。但焦点在坐标轴上的椭圆标准方程有两种情形，为了计算简便，可设方程为mx2+ny2=1(m>0，n>0)不必考虑焦点位置，求出方程即知。解：设所求椭圆的方程为mx2+ny2=1，（m>0，n>0） 点，和点，在椭圆上，AB()()32231∴·即mnmnmnmn()()()32123113411212222∴mn11515故所求椭圆的方程为。xy221551例2.已知椭圆，，是它的焦点。是过的直线xaybabFFABF222212110()与椭圆交于A、B两点，求△ABF2的周长。解析：数形结合，由椭圆定义即可求得答案。用心爱心专心解： ||||AFAFa122||||BFBFa122又 △ABF2的周长=|AB|+|BF2|+|AF2|=|AF1|+|BF1|+|AF2|+|BF2|=4a∴△ABF2的周长为4a。例3.设为椭圆上一点，到左准线的距离为，则到右准PxyPP2210036110线的距离为（）A.6B.8C.10D.15解析：法一：应用椭圆的第二定义即可求出结果为15。法二：应用椭圆的几何意义，点到两准线的距离之和为，又知到P22acP左准线距离，作差即可求出点P到右准线距离。例4.点P与定点F（2，0）的距离和它到定直线x=8的距离的比是1∶2，求点P的轨迹方程，并说明轨迹是什么图形。分析：根据椭圆的第二定义可知，动点P的轨迹是中心在原点，焦点在x轴上的椭圆，且知焦点为（－，）、（，），准线方程±，离心率。F20F20x=812e12解：依椭圆第二定义知：，，∴，caca281622∴。bac22216412∴所求椭圆的方程为。xy2216121即点的轨迹方程为：，轨迹为椭圆。Pxy2216121例5.已知点在圆：上移动，点在椭圆上移动，PCxyQxy22224141()求|PQ|的最大值。分析：做此题要数形结合，从图中可见，要求|PQ|的最大值，只要考虑圆心到椭圆上的点的距离即可，而椭圆上的点是有范围的，于是转化为二次函数在闭区间上的最值问题。设：椭圆上的一点Q（x，y），又C（0，4）。则|QC|2=x2+(y－4)241422()()yy38202yy用心爱心专心3437632()y又 ∴当时，大1115yyQC||∴|PQ|的最大值为5+1=6。例6.已知椭圆内有一点，，是椭圆的右焦点，在椭圆xyPF2243111()上求一点M，使|MP|+2|MF|的值最小，求点M的坐标。分析：|MF|是椭圆上一点到焦点的距离，根据椭圆的第二定义，有||||||||MFMMMMMF122∴∴||||||||MPMFMP...