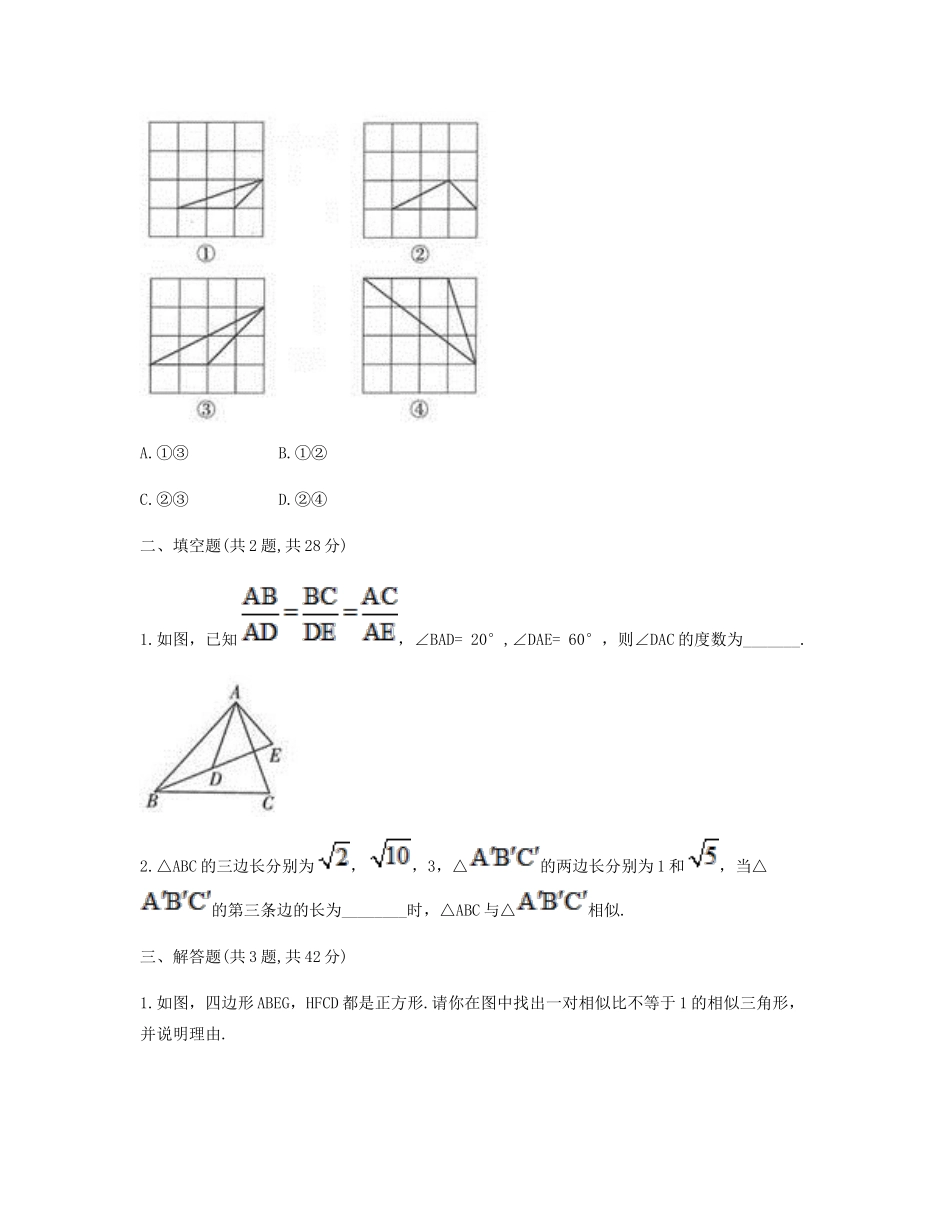
《利用三边判定三角形相似定理》A卷一、单项选择题(共2题,共30分)1.下列条件,能使△ABC和△A1B1C1,相似的是()A.AB=2.5,BC=2,AC=3;AlBl=3,B1C1=4,A1C1=6B.AB=2,BC=3,AC=4;A1B1=3,B1C1=6,A1C1=C.AB=10,BC=AC=8;A1B1=,B1C1=AlCl=D.AB=1,BC=,AC=3,A1B1=,B1C1=2,A1C1=2.如图,有四个4×4的正方形网格(每个网格中的小正方形边长都是1),每个网格中均有一个“格点三角形”(三角形的顶点都在小正方形的顶点上),则图中“格点三角形”是相似三角形的是()A.①③B.①②C.②③D.②④二、填空题(共2题,共28分)1.如图,已知,∠BAD=20°,∠DAE=60°,则∠DAC的度数为_______.2.△ABC的三边长分别为,,3,△的两边长分别为1和,当△的第三条边的长为________时,△ABC与△相似.三、解答题(共3题,共42分)1.如图,四边形ABEG,HFCD都是正方形.请你在图中找出一对相似比不等于1的相似三角形,并说明理由.2.如图,在△ABC中,点D,E,F分别是CA,AB,BC的中点.求证:△FDE∽△ABC.3.如图,已知AB∥DE,AC∥DF,BC∥EF,求证:△DEF∽△ABC.