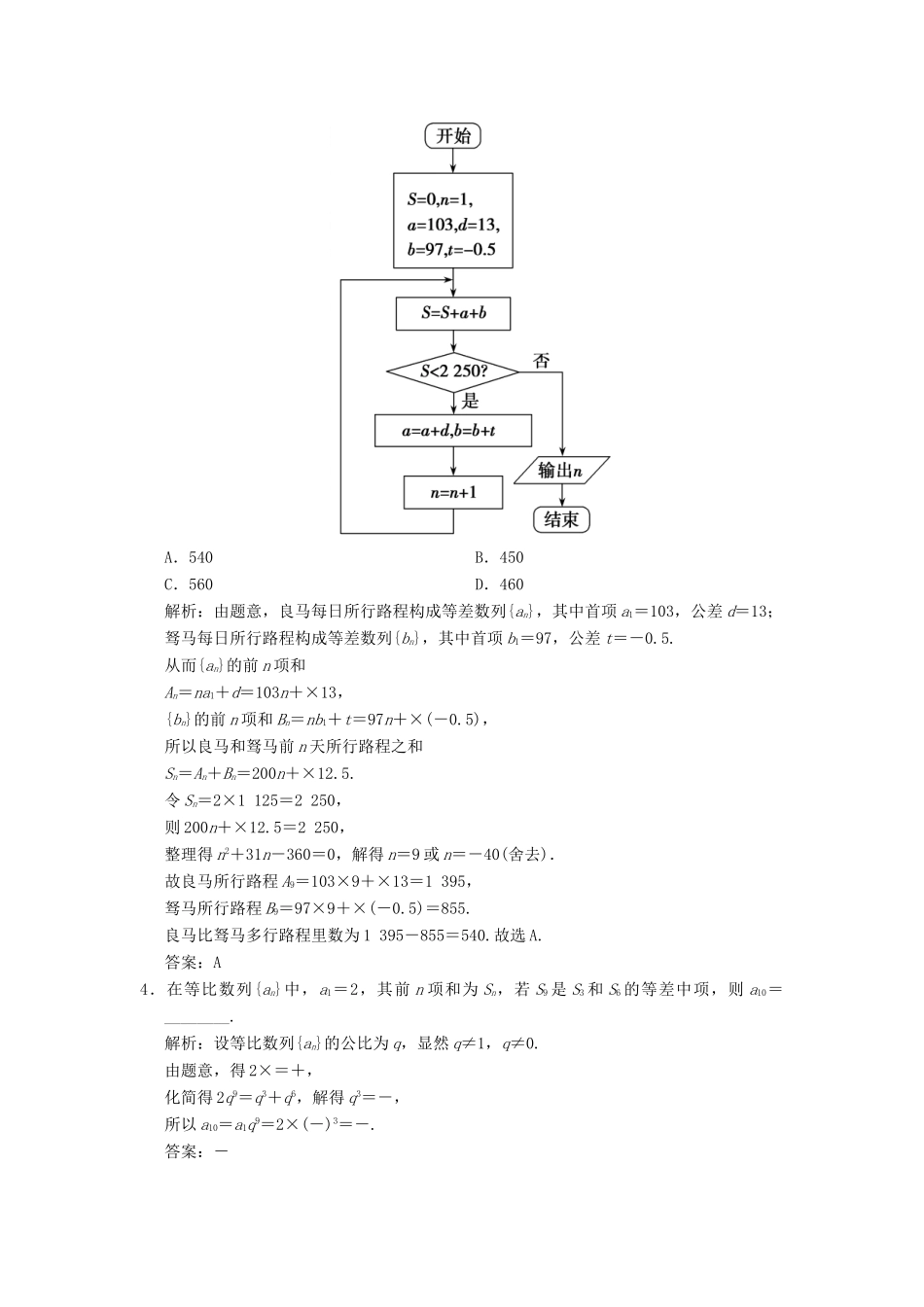
第1讲基础小题部分1.(2018·高考北京卷)设a,b,c,d是非零实数,则“ad=bc”是“a,b,c,d成等比数列”的()A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件解析:a,b,c,d是非零实数,若ad=bc,则=,此时a,b,c,d不一定成等比数列;反之,若a,b,c,d成等比数列,则=,所以ad=bc,所以“ad=bc”是“a,b,c,d成等比数列”的必要而不充分条件,故选B.答案:B2.(2017·高考全国卷Ⅱ)我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯()A.1盏B.3盏C.5盏D.9盏解析:每层塔所挂的灯数从上到下构成等比数列,记为{an},则前7项的和S7=381,公比q=2,依题意,得S7==381,解得a1=3.答案:B3.(2017·高考全国卷Ⅰ)记Sn为等差数列{an}的前n项和.若a4+a5=24,S6=48,则{an}的公差为()A.1B.2C.4D.8解析:设等差数列{an}的公差为d,则由得即解得d=4.答案:C4.(2017·高考全国卷Ⅲ)等差数列{an}的首项为1,公差不为0.若a2,a3,a6成等比数列,则{an}前6项的和为()A.-24B.-3C.3D.8解析:设等差数列{an}的公差为d,因为a2,a3,a6成等比数列,所以a2a6=a,即(a1+d)(a1+5d)=(a1+2d)2,又a1=1,所以d2+2d=0,又d≠0,则d=-2,所以a6=a1+5d=-9,所以{an}前6项的和S6=×6=-24,故选A.答案:A1.已知等比数列{xn}的公比为q,若恒有|xn|>|xn+1|,且=,则首项x1的取值范围是()A.(,1)B.(0,1)C.(0,)D.(0,)∪(,1)解析:由|xn|>|xn+1|得1>||=|q|,故-1