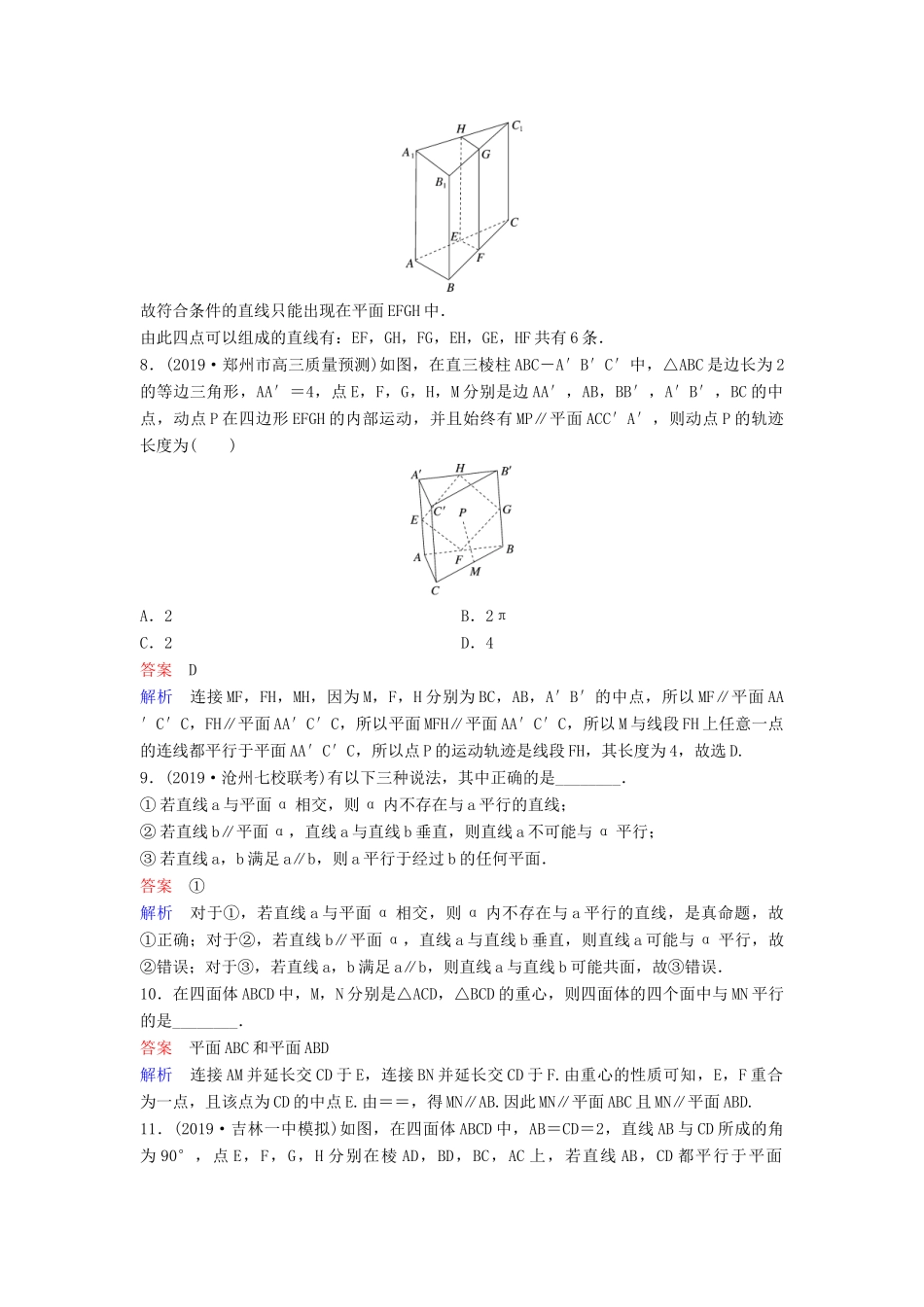
题组层级快练(五十一)1.下列关于线、面的四个命题中不正确的是()A.平行于同一平面的两个平面一定平行B.平行于同一直线的两条直线一定平行C.垂直于同一直线的两条直线一定平行D.垂直于同一平面的两条直线一定平行答案C解析垂直于同一条直线的两条直线不一定平行,可能相交或异面.本题可以以正方体为例证明.2.设α,β,γ为平面,a,b为直线,给出下列条件:①a⊂α,b⊂β,a∥β,b∥α;②α∥γ,β∥γ;③α⊥γ,β⊥γ;④a⊥α,b⊥β,a∥b.其中能推出α∥β的条件是()A.①②B.②③C.②④D.③④答案C3.若空间四边形ABCD的两条对角线AC,BD的长分别是8,12,过AB的中点E且平行于BD,AC的截面四边形的周长为()A.10B.20C.8D.4答案B解析设截面四边形为EFGH,F,G,H分别是BC,CD,DA的中点,∴EF=GH=4,FG=HE=6.∴周长为2×(4+6)=20.4.(2019·安徽毛坦厂中学月考)如图,在正方体ABCD-A1B1C1D1中,E,F分别为棱AB,CC1的中点,在平面ADD1A1内且与平面D1EF平行的直线()A.有无数条B.有2条C.有1条D.不存在答案A解析因为平面D1EF与平面ADD1A1有公共点D1,所以两平面有一条过D1的交线l,在平面ADD1A1内与l平行的任意直线都与平面D1EF平行,这样的直线有无数条,故选A.5.(2019·陕西西安模拟)在空间四边形ABCD中,E,F分别为AB,AD上的点,且AE∶EB=AF∶FD=1∶4,H,G分别是BC,CD的中点,则()A.BD∥平面EFG,且四边形EFGH是平行四边形B.EF∥平面BCD,且四边形EFGH是梯形C.HG∥平面ABD,且四边形EFGH是平行四边形D.EH∥平面ADC,且四边形EFGH是梯形答案B解析如图,由条件知,EF∥BD,EF=BD,HG∥BD,HG=BD,∴EF∥HG,且EF=HG,∴四边形EFGH为梯形. EF∥BD,EF⊄平面BCD,BD⊂平面BCD,∴EF∥平面BCD. 四边形EFGH为梯形,∴线段EH与FG的延长线交于一点,∴EH不平行于平面ADC.故选B.6.(2019·衡水中学调研卷)如图,P为平行四边形ABCD所在平面外一点,E为AD的中点F为PC上一点,当PA∥平面EBF时,=()A.B.C.D.答案D解析连接AC交BE于G,连接FG,因为PA∥平面EBF,PA⊂平面PAC,平面PAC∩平面BEF=FG,所以PA∥FG,所以=.又AD∥BC,E为AD的中点,所以==,所以=.7.(2019·蚌埠联考)过三棱柱ABC-A1B1C1的任意两条棱的中点作直线,其中与平面ABB1A1平行的直线共有()A.4条B.6条C.8条D.12条答案B解析作出如图的图形,E,F,G,H是相应棱的中点,故符合条件的直线只能出现在平面EFGH中.由此四点可以组成的直线有:EF,GH,FG,EH,GE,HF共有6条.8.(2019·郑州市高三质量预测)如图,在直三棱柱ABC-A′B′C′中,△ABC是边长为2的等边三角形,AA′=4,点E,F,G,H,M分别是边AA′,AB,BB′,A′B′,BC的中点,动点P在四边形EFGH的内部运动,并且始终有MP∥平面ACC′A′,则动点P的轨迹长度为()A.2B.2πC.2D.4答案D解析连接MF,FH,MH,因为M,F,H分别为BC,AB,A′B′的中点,所以MF∥平面AA′C′C,FH∥平面AA′C′C,所以平面MFH∥平面AA′C′C,所以M与线段FH上任意一点的连线都平行于平面AA′C′C,所以点P的运动轨迹是线段FH,其长度为4,故选D.9.(2019·沧州七校联考)有以下三种说法,其中正确的是________.①若直线a与平面α相交,则α内不存在与a平行的直线;②若直线b∥平面α,直线a与直线b垂直,则直线a不可能与α平行;③若直线a,b满足a∥b,则a平行于经过b的任何平面.答案①解析对于①,若直线a与平面α相交,则α内不存在与a平行的直线,是真命题,故①正确;对于②,若直线b∥平面α,直线a与直线b垂直,则直线a可能与α平行,故②错误;对于③,若直线a,b满足a∥b,则直线a与直线b可能共面,故③错误.10.在四面体ABCD中,M,N分别是△ACD,△BCD的重心,则四面体的四个面中与MN平行的是________.答案平面ABC和平面ABD解析连接AM并延长交CD于E,连接BN并延长交CD于F.由重心的性质可知,E,F重合为一点,且该点为CD的中点E.由==,得MN∥AB.因此MN∥平面ABC且MN∥平面ABD.11.(2019·吉林一中模拟)如图,在四面体ABCD中,AB=CD=2,直线AB与CD所成的角为90°,点E,F,G,H分别在棱AD,BD,BC,AC上...