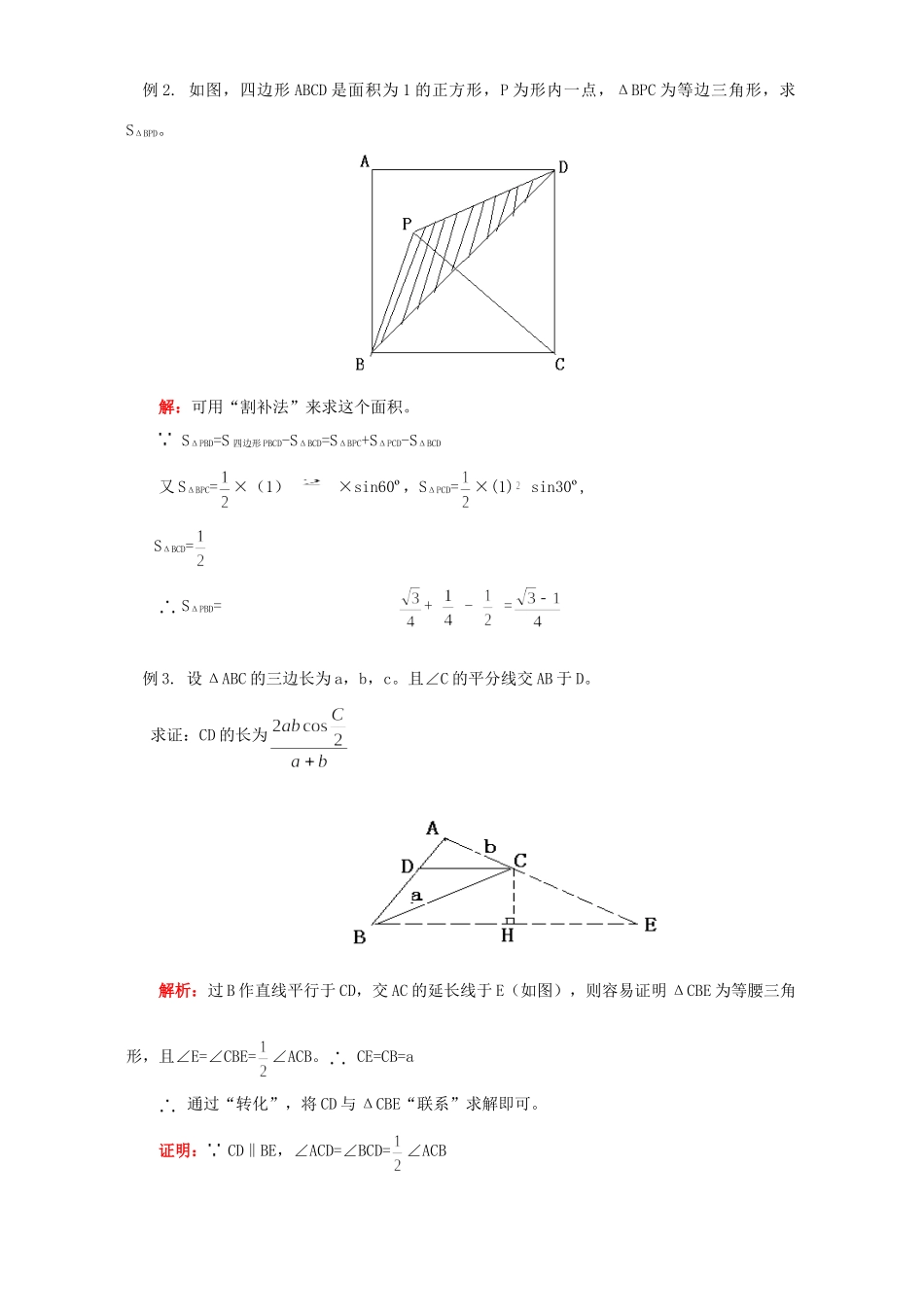
初三数学解直角三角形的应用知识精讲二一.本周教学内容:解直角三角形的应用(二)二.重点、难点:1.理解并掌握直角三角形的四种基本类型。2.通过转化,灵活应用直角三角形的知识求解应用题。【知识回顾】一.解直角三角形的四种基本类型1.已知两条直角边,解三角形2.已知一条直角边和斜边,解三角形3.已知一条直角边和一个锐角,解三角形4.已知斜边和一个锐角,解三角形二.解直角三角形的方法1.“有弦用弦,无弦用切,宁乘毋除,取原避中”意即:有斜边则用正、余弦,无斜边用正、余切,能用乘法计算时尽量不用除法计算,若既可用已知数据也可用中间过程得出的数据时,则取“原始”而不用“中间数据”2.“非转直”意即:对于非直角三角形的图形,可添加适当的辅助线把它们分割成直角三角形和矩形来计算。【典型例题】例1.平行四边形的边长分别为3和6,一个内角为120,求它的两条高线的长。解析:只须构造以两条高线为直角边的两个直角三角形。通过“平行四边形邻角互补”以及“已知斜边和一个锐角”求解即可。平行四边形的两条高线长分别为h=3sin60º=和h=6sin60º=9例2.如图,四边形ABCD是面积为1的正方形,P为形内一点,ΔBPC为等边三角形,求SΔBPD。解:可用“割补法”来求这个面积。SΔPBD=S四边形PBCD-SΔBCD=SΔBPC+SΔPCD-SΔBCD又SΔBPC=×(1)×sin60º,SΔPCD=×(1)sin30º,SΔBCD=SΔPBD=+-=例3.设ΔABC的三边长为a,b,c。且∠C的平分线交AB于D。求证:CD的长为解析:过B作直线平行于CD,交AC的延长线于E(如图),则容易证明ΔCBE为等腰三角形,且∠E=∠CBE=∠ACB。CE=CB=a通过“转化”,将CD与ΔCBE“联系”求解即可。证明:CD‖BE,∠ACD=∠BCD=∠ACB∠E=∠CBE=∠ACBCE=CB=a又由“平行线分线段成比例”定理:即:过C作CH⊥BE于H,则RtΔCBH中,BH=BE=acosBE=2BH=2acos,CD=例4.是否存在这样的实数k,使得方程8x-2kx+k-1=0的两个实数根为一个直角三角形的两个锐角的正弦?若存在,求出k的值;否则,请说明理由解:对这一类“是否存在”型的数学问题,我们一般是先假设“存在”,然后据此严格论证。如若推理步步有据,逻辑严密,则必可得出存在的那个k的值;如若推理过程出现逻辑错误,则应否定假设的存在,从而说明“不存在”∴若存在这样的实数k,则设直角三角形的两锐角为A、B,cosA=sinB由题意,得Δ≥0∵Δ=4k-32(k-1)=4[k-8(k-1)]≥0∴k-8k+8=(k-4+2)(k-4-2)≥0∴k≤4-2或k≥4+2又∴∴k>1∴10)∴sinB=∠C=90∴sinC=1∴代入求解计算即可6.当时,△ADF与△DEB的面积和为最小,最小值为提示:设AD=x,则DF=x,BD=1-x,DE=∴y=S,代入相关数据,可求解得y=(0