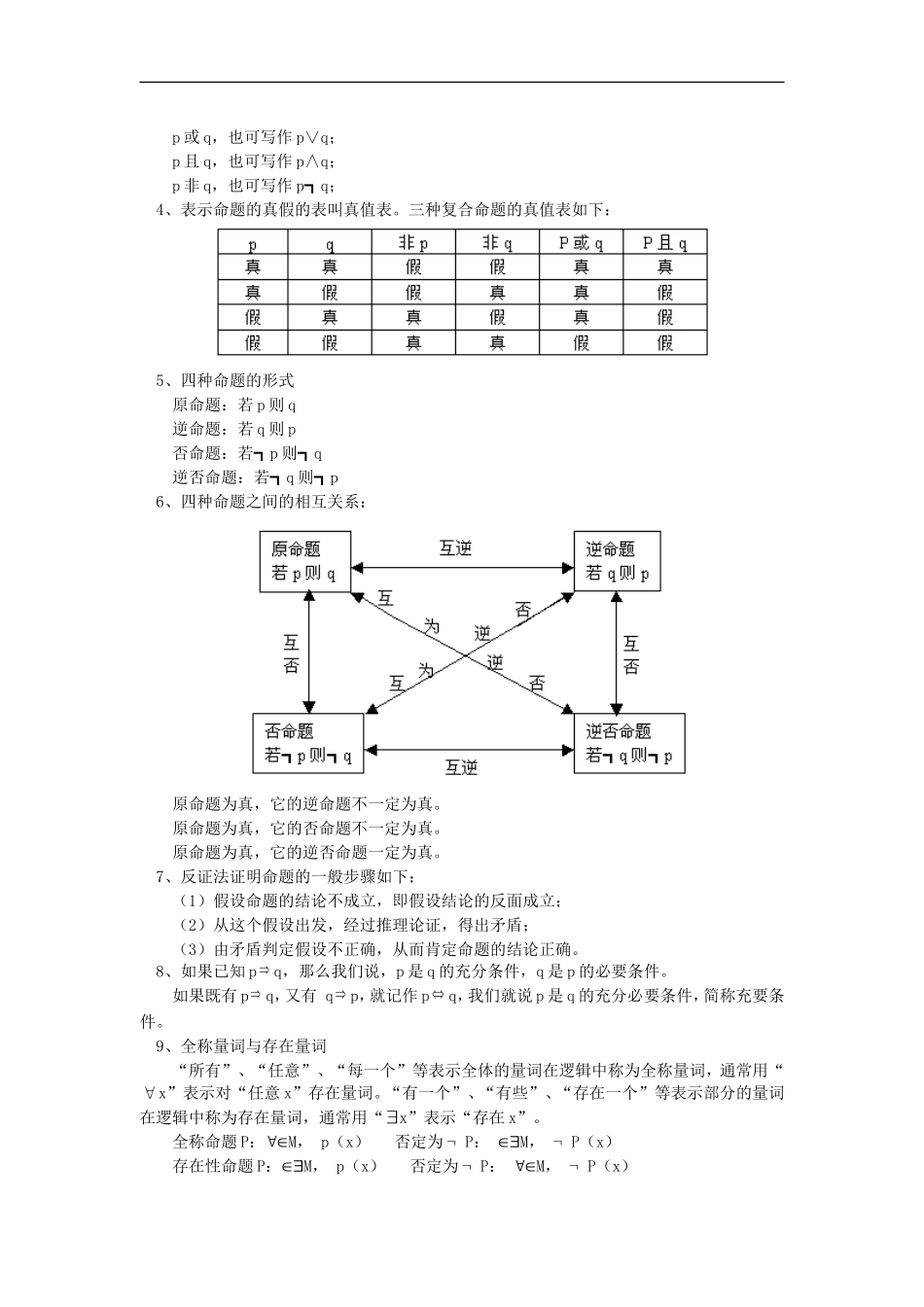
高二数学常用逻辑用语苏教版【本讲教育信息】一.教学内容:常用逻辑用语二.重点、难点:教学重点:1、掌握命题之间的关系,以及充要条件的证明。2、理解逻辑联结词及含有一个量词的命题的否定。教学难点:充要条件及反证法的证明三.本章知识结构:EMBEDWord.Picture.8常用逻辑用语命题及其关系简单的逻辑联结词全称量词与存在量词四种命题充分条件与必要条件量词全称量词存在量词含有一个量词的否定或且非并集交集补集运算四.基本内容梳理:1、可以判断真假的语句叫做命题。命题有真有假,其中正确的命题叫做真命题,错误的命题叫做假命题。语句是不是命题,关键在于能不能判断其真假,也就是判断其是否成立,不能判断真假的语句,就不能叫命题。2、“或”、“且”、“非”这些词叫做逻辑联结词。如果命题中不含逻辑联结词,那么我们把这样的命题叫做简单命题。由简单命题与逻辑联结词构成的命题叫做复合命题。3、我们常用小写的拉丁字母p,q,r,s,…来表示命题。“或”的符号是“∨”,“且”的符号是“∧”,“非”的符号是“┓”。三种复合命题形式分别是:p或q,也可写作p∨q;p且q,也可写作p∧q;p非q,也可写作p┓q;4、表示命题的真假的表叫真值表。三种复合命题的真值表如下:5、四种命题的形式原命题:若p则q逆命题:若q则p否命题:若┓p则┓q逆否命题:若┓q则┓p6、四种命题之间的相互关系:原命题为真,它的逆命题不一定为真。原命题为真,它的否命题不一定为真。原命题为真,它的逆否命题一定为真。7、反证法证明命题的一般步骤如下:(1)假设命题的结论不成立,即假设结论的反面成立;(2)从这个假设出发,经过推理论证,得出矛盾;(3)由矛盾判定假设不正确,从而肯定命题的结论正确。8、如果已知pq,那么我们说,p是q的充分条件,q是p的必要条件。如果既有pq,又有qp,就记作pq,我们就说p是q的充分必要条件,简称充要条件。9、全称量词与存在量词“所有”、“任意”、“每一个”等表示全体的量词在逻辑中称为全称量词,通常用“x”表示对“任意x”存在量词。“有一个”、“有些”、“存在一个”等表示部分的量词在逻辑中称为存在量词,通常用“x”表示“存在x”。全称命题P:"ÎM,p(x)否定为ØP:Î$M,ØP(x)存在性命题P:Î$M,p(x)否定为ØP:"ÎM,ØP(x)【典型例题】例1.命题p:正方形ABCD是圆内接四边形。命题q:正方形ABCD是平行四边形。分别写出下列各种形式的复合命题:(1)p或q;(2)p且q;(3)非p;(4)非q解:(1)正方形ABCD是圆内接四边形或平行四边形。(2)正方形ABCD是圆内接四边形且平行四边形。(3)正方形ABCD不是圆内接四边形。(4)正方形ABCD不是平行四边形。例2.如果命题“p且q”与命题“p或q”都是假命题,判断复合命题“非p”和“非q”的真假。解:由命题“p且q”是假命题,得“命题p”和“命题q”至少有一个是假命题。由命题“p或q”为假命题,得“命题p”和“命题q”都是假命题。所以命题“非p”是真命题,命题“非q”也是真命题。例3.已知原命题为“若a=c,b=d,则a+b=c+d”,写出它的逆命题,否命题和逆否命题,并判断其真假。解:原命题“若a=c,b=d,则a+b=c+d”是真命题。逆命题“若a+b=c+d,则a=c,b=d”是假命题。否命题“若a≠c或b≠d,则a+c≠b+d”是假命题。逆否命题“若a+b≠c+d,则a≠c或b≠d”是真命题。例4.写出下列命题的否定(1)对任意的正数x,>x-1;(2)不存在实数x,x2+1<2x;(3)已知集合AÍB,如果对于任意的元素x∈A,那么x∈B;(4)已知集合AÍB,存在至少一个元素x∈B,使得x∈A;解:(1)存在正数x,≤x-1;(2)存在实数x,x2+1<2x;(3)已知集合AÍB,存在元素x∈A,那么xB;(4)已知集合AÍB,任意一个元素x∈B,使得xA;例5.判断下列各组命题是否为等价命题,说明理由:(1)“若A则B”与“若┓A则┓B”;(2)“若B则A”与“若┓A则┓B”;(3)“若┓B则┓A”与“若┓A则┓B”;(4)“若┓A则┓B”与“若B则A”。解:(1)是互否命题,它们不是等价命题。(2)是互为逆否命题,它们是等价命题。(3)是互逆命题,它们不是等价命题。(4)是互为逆...