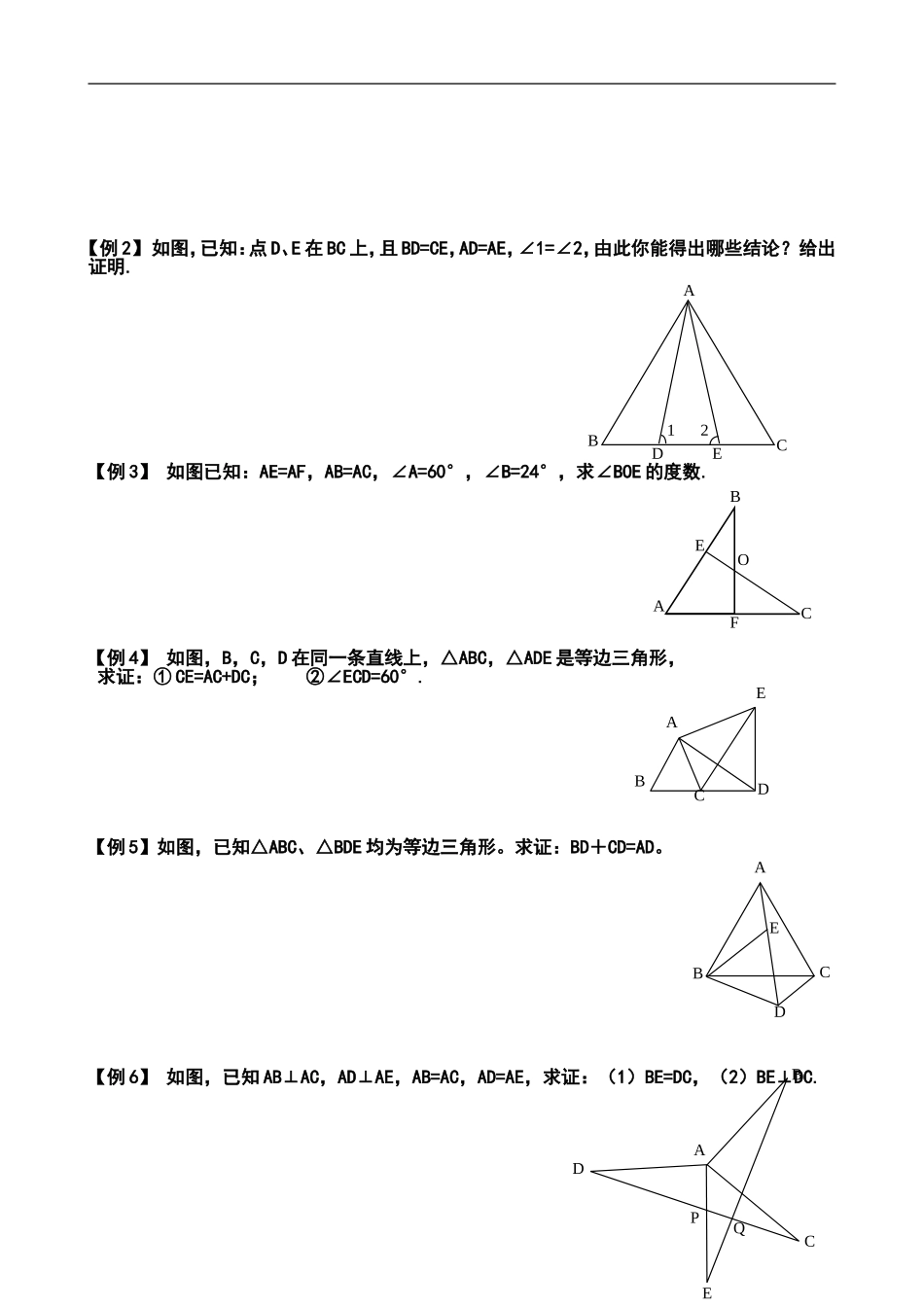
全等三角形(二)【励志故事】给中国大学生的五封信前段时间,原微软副总裁李开复博士被Google公司任命为全球副总裁兼中国区总裁,引起了包括《纽约时报》、《参考消息》等全球上万家媒体的追逐报道。如今,李开复博士极为关注中国教育的发展,曾亲自给中国大学生写了5封饱含关切之情的来信之后,引起了极大的反响。以下为五封信的选摘:第四封信:大学应这样过就读大学时,你应当掌握七项学习,包括自修之道、基础知识、实践贯通、培养兴趣、积极主动、掌控时间、为人处世。经过大学四年,你会从思考中确立自我,从学习中寻求真理,从独立中体验自主,从计划中把握时间,从表达中锻炼口才,从交友中品味成熟,从实践中赢得价值,从兴趣中获取快乐,从追求中获得力量。离开大学时,只要做到了这些,你最大的收获将是“对什么都可以拥有的自信和渴望”。你就能成为一个有潜力、有思想、有价值、有前途的中国未来的主人翁。【知识要点】定义:两边和它们的夹角对应相等的两个三角形全等,简写成“边角边”或“SAS”,几何表示如图,在和中,≌【典型例题】【例1】已知:如图,AB=AC,AD=AE,求证:BE=CD.ABCEDFADBEC【例2】如图,已知:点D、E在BC上,且BD=CE,AD=AE,∠1=∠2,由此你能得出哪些结论?给出证明.【例3】如图已知:AE=AF,AB=AC,∠A=60°,∠B=24°,求∠BOE的度数.【例4】如图,B,C,D在同一条直线上,△ABC,△ADE是等边三角形,求证:①CE=AC+DC;②∠ECD=60°.【例5】如图,已知△ABC、△BDE均为等边三角形。求证:BD+CD=AD。【例6】如图,已知AB⊥AC,AD⊥AE,AB=AC,AD=AE,求证:(1)BE=DC,(2)BE⊥DC.ABDEC12BEAFCOEABCDDABQCPEDABCE【巩固练习】1.在△ABC和△中,若AB=,AC=,还要加一个角的条件,使△ABC≌△,那么你加的条件是()A.∠A=∠B.∠B=∠C.∠C=∠D.∠A=∠2.下列各组条件中,能判断△ABC≌△DEF的是()A.AB=DE,BC=EF;CA=CDB.CA=CD;∠C=∠F;AC=EFC.CA=CD;∠B=∠ED.AB=DE;BC=EF,两个三角形周长相等3.阅读理解题:如图:已知AC,BD相交于O,OA=OB,OC=OD.那么△AOD与△BOC全等吗?请说明理由.△ABC与△BAD全等吗?请说明理由.小明的解答:△AOD≌△BOC而BAD=△AOD+△ADB△ABC+△BOC+△AOB所以△ABC≌△BAD(1)你认为小明的解答有无错误;(2)如有错误给出正确解答;4.如图,点C是AB中点,CD∥BE,且CD=BE,试探究AD与CE的关系。5.如图,AE是AB=AC(1)若D是AE上任意一点,则△ABD≌△ACD,说明理由.DC12OAB—ACBEDSASOA=OBOD=OC(2)若D是AE反向延长线上一点,结论还成立吗?请说明理由.6.如图,已知AB=AC,EB=EC,请说明BD=CD的理由【思考题】1.如图,已知AB=AC,AD=AE,BF=CF,求证:≌。2.如图,△ABC,△BDF为等腰直角三角形。求证:(1)CF=AD;(2)CE⊥AD。3.如图,AB=AC,AD=AE,BE和CD相交于点O,AO的延长线交BC于点F。求证:BF=FC。BCDEA12ABEDCABCEDFACBDEFADECBFO全等三角形(二)作业姓名________成绩________1.已知:如图1,AD∥BC,AE=CF,AD=BC,E、F在直线AC上,求证:DE∥BF。2.如图,△ABC,△BDF为等腰直角三角形,求证:(1)CF=AD;(2)CE⊥AD。3.已知:如图2,AD∥BC,AE=CF,AD=BC,E、F在直线AC上,求证:DE∥BF。12DCABEF图1ACBDEF12DCABEF图2