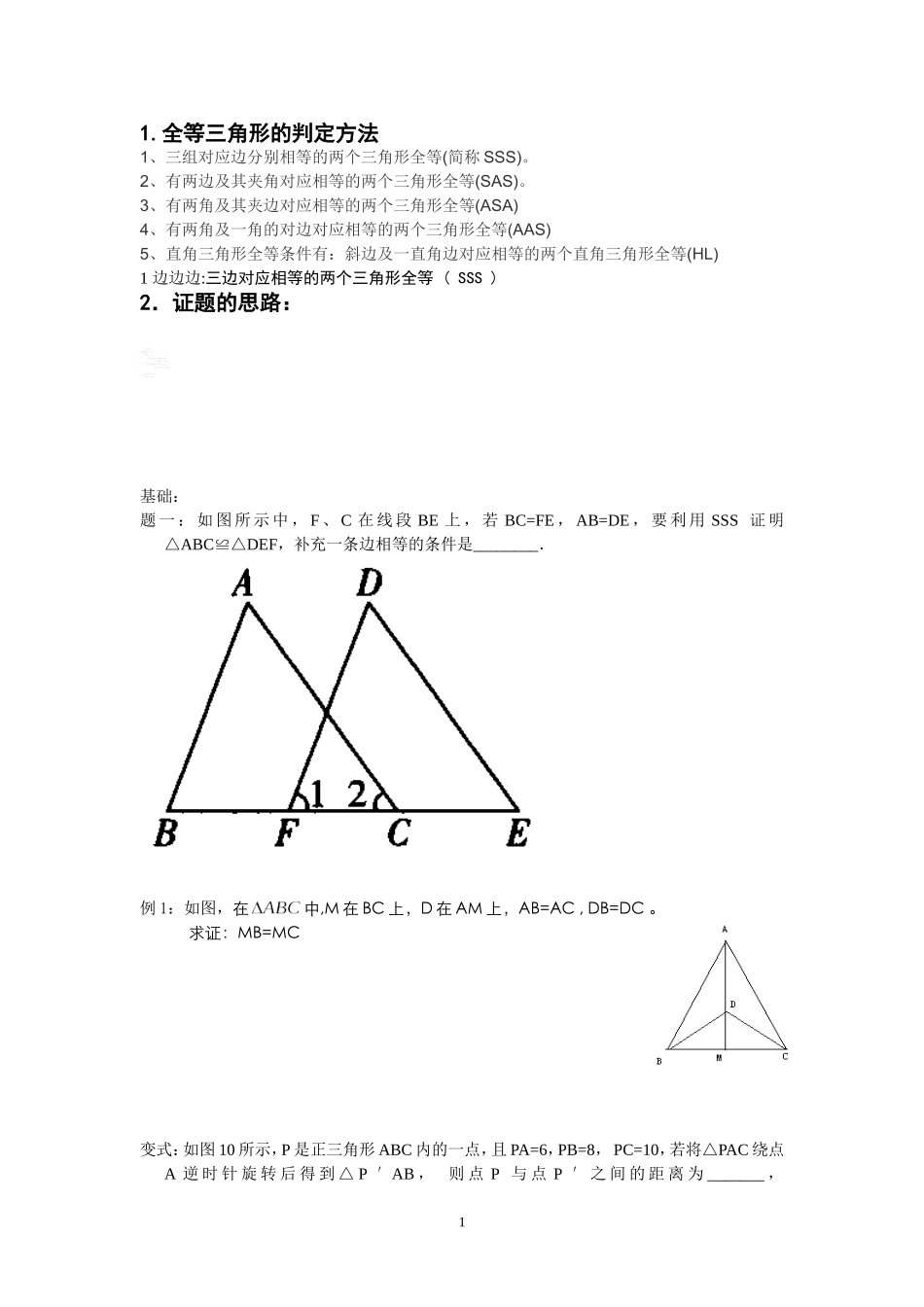
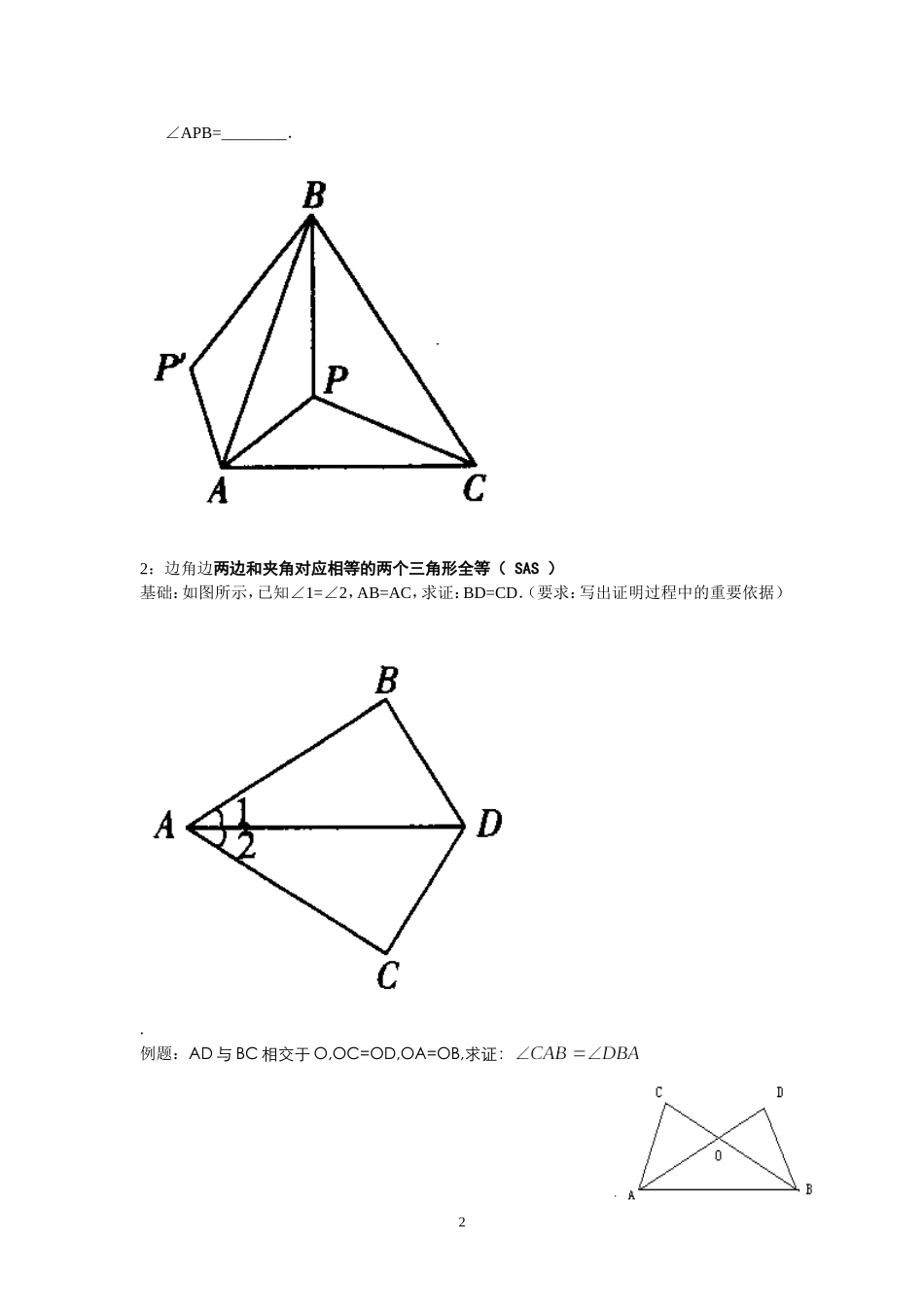
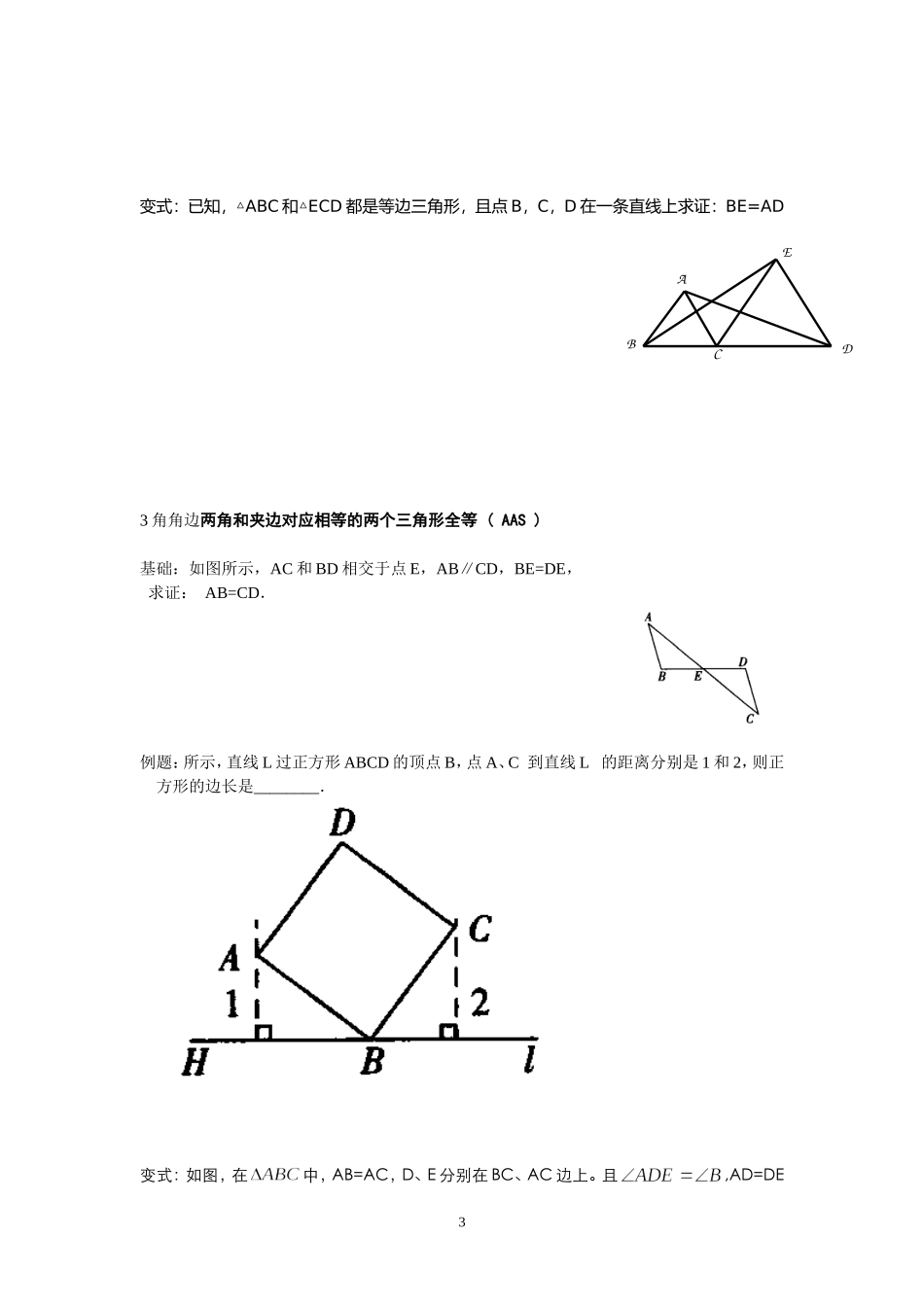
11.全等三角形的判定方法1、三组对应边分别相等的两个三角形全等(简称SSS)。2、有两边及其夹角对应相等的两个三角形全等(SAS)。3、有两角及其夹边对应相等的两个三角形全等(ASA)4、有两角及一角的对边对应相等的两个三角形全等(AAS)5、直角三角形全等条件有:斜边及一直角边对应相等的两个直角三角形全等(HL)1边边边:三边对应相等的两个三角形全等(SSS)2.证题的思路:基础:题一:如图所示中,F、C在线段BE上,若BC=FE,AB=DE,要利用SSS证明△ABC≌△DEF,补充一条边相等的条件是________.例1:如图,在中,M在BC上,D在AM上,AB=AC,DB=DC。求证:MB=MC变式:如图10所示,P是正三角形ABC内的一点,且PA=6,PB=8,PC=10,若将△PAC绕点A逆时针旋转后得到△P′AB,则点P与点P′之间的距离为_______,2∠APB=________.2:边角边两边和夹角对应相等的两个三角形全等(SAS)基础:如图所示,已知∠1=∠2,AB=AC,求证:BD=CD.(要求:写出证明过程中的重要依据).例题:AD与BC相交于O,OC=OD,OA=OB,求证:3变式:已知,△ABC和△ECD都是等边三角形,且点B,C,D在一条直线上求证:BE=AD3角角边两角和夹边对应相等的两个三角形全等(AAS)基础:如图所示,AC和BD相交于点E,AB∥CD,BE=DE,求证:AB=CD.例题:所示,直线L过正方形ABCD的顶点B,点A、C到直线L的距离分别是1和2,则正方形的边长是________.变式:如图,在中,AB=AC,D、E分别在BC、AC边上。且,AD=DEEDCAB4基础:求证:≌.4角边角两角和夹边对应相等的两个三角形全等(ASA)基础:如图,梯形ABCD中,AB//CD,E是BC的中点,直线AE交DC的延长线于F求证:≌变式:如图所示,已知∠1=∠2,∠3=∠4.求证:AB=AC.55一条直角边和斜边对应相等的两个直角三角形全等(HL)基础:如图5所示,我们可以用三角板来平分一个任意的锐角,在已知△AOB的两边上分别取OM=ON,再分别过点M、N作OA、OB的垂线,交点为P,画射线OP,OP就是∠AOB的平分线,说明其中的道理.例题:如图,在中,,沿过点B的一条直线BE6折叠,使点C恰好落在AB变的中点D处,则∠A的度数=。角平分线1)。角平分线性质定理:角平分线上的点到这个角两边的距离相等。逆定理:到一个叫两边的距离相等的点在这个角的平分线上基础:如图,在中,,平分,,那么点到直线的距离是cm.线段垂直平分线的性质基础:如图4所示,△ABC中,AB=8,DE垂直平分BC,若△AEC周长为13,则AC=______.尺规作图ABDC7例题:如图,Rt△ABC中,∠C=90°,∠CAB=30°,用圆规和直尺作图,用两种方法把它分成两个三角形,且其中一个是等腰三角形.(保留作图痕迹,不要求写作法和证明).思考如图所示,已知:∠AOB,点M、N.求作:点P,使点P在∠AOB的平分线上,且PM=PN(要求:用尺规作图,保留作图痕迹,不写作法).ABCCBA