高中数学 221(平面向量基本定理)课件(1) 新人教B版必修4 课件VIP免费

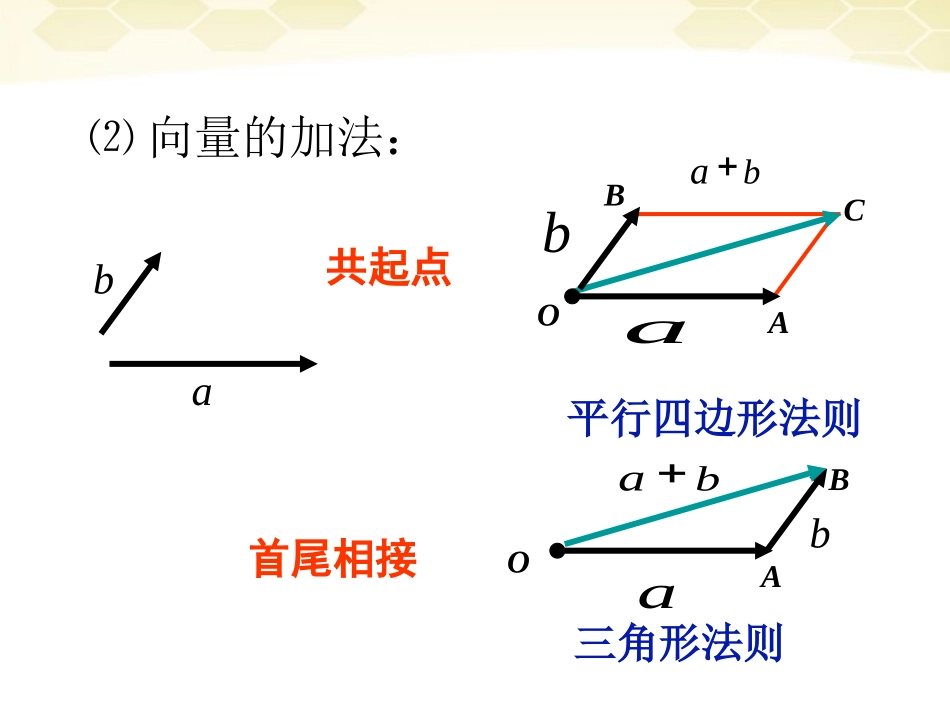
平面向量基本定理非零向向量与量ba共线,当时，0与同向，ba且是的倍;||b||a当时，0与反向，ba且是的倍;||b||a||当时，00b，且.||0b有且只有一个实数λ，使得b=λa.⑴向量共线充要条件复习:ab⑵向量的加法：OBCAabOAaBbbaba平行四边形法则三角形法则共起点首尾相接问题：（1）向量a是否可以用含有e1、e2的式子来表示呢？怎样表示？（2）若向量a能够用e1、e2表示，这种表示是否唯一？请说明理由.引入:1e�2e�OCABMNOCOMON�如图111OMOAe�1122OCee�1122+aee��即222ONOBe�a�12思考：一个平面内的两个不共线的向量e、e与该平面内的任一向量a之间的关系.新课:1e�2e�OCABMNaOCOMON�如图111OMOAe�1122OCee�1122+aee��即222ONOBe�1122+aee����1122这就是说平面内任一向量a都可以表示成λe+λe的形式平面向量基本定理如果e1、e2是平面内的两个不共线向量，那么对于这一平面内的任一向量a，有且只有一对实数a1、a2，使1122aaaee说明：①e1、e2是两个不共线的向量；②a是平面内的任一向量；③a1，a2实数，唯一确定.∵�OAOMON∴存在实数a1，a2使11OMa�e,22ONa�e.于是1122.aaaee设存在实数x,y使12xyaee，只要证1ax且2ayNMOe2e1Aa1e1+a2e2=xe1+ye2,(x－a1)e1+(y－a2)e2=0(存在性)(唯一性)我们把不共线向量e1，e2叫做这一平面内所有向量的一组基底，记为{e1，e2}，a1e1+a2e2叫做向量a关于基底{e1，e2}的分解式。例1.已知平行四边形ABCD的两条对角线相交于M，设，，试用基底{a，b}表示ABa�ADb�,,,�MAMBMCMDbaMDCBA实例:例2.已知A,B是l上任意两点，O是l外一点，求证：对直线l上任一点P，存在实数t，使关于基底{}的分解式为OP�,OAOB�(1).OPtOAtOB�POBA根据平面向量基本定理，同一平面内任一向量都可以用两个不共线的向量表示，再由已知可得OPOAAP�OAtAB�()�OAtOBOA(1)OPtOAtOB�即1()2�OMOAOB特殊地，令t=,点M是AB的中点，则12例3.已知平行四边形ABCD中,M,N分别是DC,BC的中点且，用表示.,AMcANd�,cd��,ABAD�DBCANM解：设,�ABaADb1212cbadab�42334233adcbcd����例4.已知向量不共线，如果向量与共线,求λ.12,�ee12ee�12ee�解：由已知得1212()�eeee所以1解得λ=±1.��1.在ABCD中，设AC=a,BD=b,则AB=,AD=.(用a、b来表示)练习:2ab2abBACDCCBBAADDEEFFGG22、设、设GG是△是△ABCABC的重心，若的重心，若CA=a,CB=bCA=a,CB=b试用试用a,ba,b表示表示AGAGAABBCCDDEEFF33、在正六边形、在正六边形ABCDEFABCDEF中，中，AC=a,AC=a,AD=bAD=b用用a,ba,b表示向量表示向量ABAB、、BCBC、、CDCD、、DEDE、、EFEF、、FAFA。。OO�（高考实战）(2007江西)如图,在ΔABC中,点O是BC的中点,过点O的直线分别交直线AB,AC于不同的两点M,N,若AB=mAM,AC=nAN,则m+n的值为____:____.ABCMNO2课堂小结:平面向量基本定理：�12这里不共线的向量e、e叫做表示这一平面内所有向量的一组基底.���12121122如果e、e是同一平面内的两个不共线的向量，那么对于这一平面内的任一向量a，有且只有一对实数λ、λ，可使a=λe+λe��12112212一个平面向量用一组基底e,e表示成ａ=λe+λe的形式，我们称它为向量的分解。当e,e互相垂直时，就称为向量的正交分解。