高中数学几种不同增长的函数模型课件 新课标 人教版 必修1A 课件VIP免费

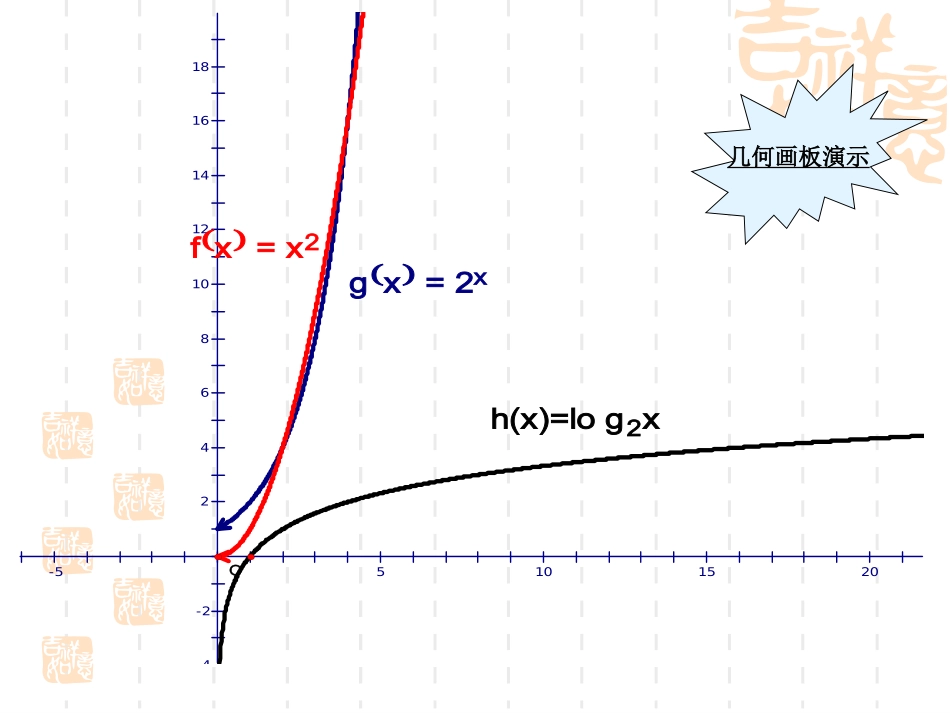
.),0()0()1(),1(log上都是增函数在区间与幂函数指数函数对数函数nxyaayaxynxa从上节课的两个例子中可以看到，这三类函数的增长是有差异的，那么，这种差异的具体情况到底怎么样呢？:log,,222的图象在同一坐标系画出函数xyxyyx18161412108642-2-4-55101520h(x)=log2xgx=2xfx=x2O几何画板演示结论1：一般地，对于指数函数y=ax(a>1)和幂函数y=xn(n>0)，通过探索可以发现：在区间(0,+∞)上，无论n比a大多少，尽管在x的一定范围内，ax会小xn，但由于ax的增长快于xn的增长，因此总存在一个x0，当x>x0时，就会有ax>xn.结论2：一般地，对于指数函数y=logax(a>1)和幂函数y=xn(n>0)，通过探索可以发现：在区间(0,+∞)上，随着x的增大，logax增大得越一越慢，图象就像是渐渐地与x轴平行一样。尽管在x的一定范围内，logax可能会小xn，但由于logax的增长慢于xn的增长，因此总存在一个x0，当x>x0时，就会有logax1)，y=logax(a>1)和y=xn(n>0)都是增函数。(2)、随着x的增大，y=ax(a>1)的增长速度越来越快，会远远大于y=xn(n>0)的增长速度。(3)、随着x的增大，y=logax(a>1)的增长速度越来越慢，会远远大于y=xn(n>0)的增长速度。总存在一个x0，当x>x0时，就有logax