高中数学 平面向量基本定理课件 北师大版必修4 课件VIP免费

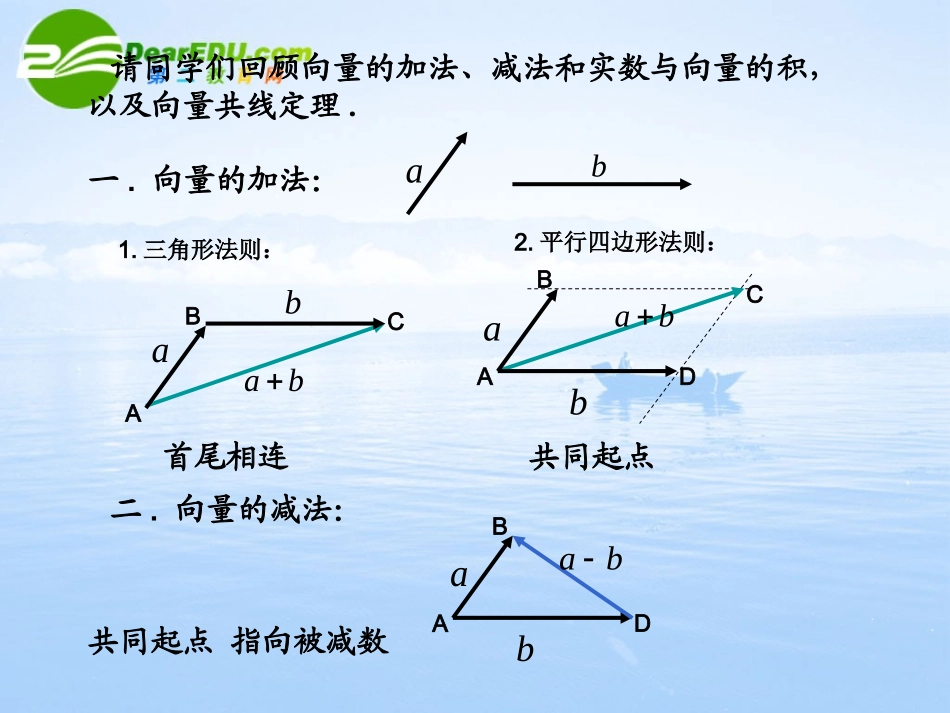
平面向量基本定理奎屯王新敞新疆教学目的：教学重点：教学难点：1．了解平面向量基本定理的证明．2.掌握平面向量基本定理及其应用.奎屯王新敞新疆奎屯王新敞新疆奎屯王新敞新疆奎屯王新敞新疆平面向量基本定理的应用.平面向量基本定理的理解.请同学们回顾向量的加法、减法和实数与向量的积，以及向量共线定理.1.三角形法则：2.平行四边形法则：CBAABCD一.向量的加法：首尾相连共同起点ababaabbbab二.向量的减法：BADaba共同起点指向被减数1.当时：02.当时：03.当时：0与方向相同。ba方向：长度：ba与方向相反。ba00ba二、向量共线定理:向量与非零向量共线的充要条件是有且只有一个实数，使得：baba今天我们继续来学习有关向量的知识：设、是同一平面内的两个不共线的向量，是这一平面内的向量，我们研究与、之间的关系？abccab首先，请大家在用平行四边形法则作出、、ab2ab2ababca+2bbabCD'ABDa2a+babCB'ABDa+babCABDbBaOAMNcC我们一起来作图（平行四边形法则：起点相同）㈠在平面内任取一点O，作,,OAaOBbOCc�㈡过点C作平行于直线OB的直线，与直线OA相交于M；过点C作平行于直线OA的直线，与直线OB相交于N；你们得到了什么？OMONOC�现在要找与，与的关系，它们有什么样的关系呢？OM�OA�OB�ON�原来与共线；与共线。OM�OA�OB�ON�思考：我们能否用，把表示出来呢？abc所以有且只有一个实数,使得：11OMOA�2ONOB�有且只有一个实数,使得：2即12OCOAOB�12cab思考2：是否这一平面内的任一向量都可以用，来表示呢？ab我们作图验证演示12ab这样，以与为基础，我们可以表示这一平面内的所有向量，我们就把这两个向量叫做：表示这一平面内所有向量的基底.ab(2)对你给的这两个向量有什么要求？思考3：(1)这一平面内所有向量的基底是否唯一呢？大家作图验证是否可以由其它两个向量来表示？c演示我们得到：(1)基底不唯一；(2)要求这两个向量不共线；(3)如果基底选定，则，唯一确定,可以为零.12(3)如果基底选定，，能唯一确定吗？能为零吗?12我们得到：这一平面内的任一向量都可以表示成：c既然这两个向量这么特别，我们一般用，表示.1e�2e�通过我们的努力，得到了：平面向量基本定理如果，是同一平面内的两个不共线向量，那么对于这一平面内的任一向量，有且只有一对实数，，使1e�2e�a121122aee��我们把不共线的向量，叫做表示这一平面内所有向量的一组基底.1e�2e�特别的：时,1200a时,，与共线.120,011ae��a1e�时,，与共线.120,022ae��a2e�例1课堂练习：P118练习1已知向量、，求作向量.1e�2e�122.53ee�1e�2e�作法:(1)任取一点O,作(2)作平行四边形OACBBOAC12.5OAe�23OBe�于是就是.OC�122.53ee�baMCABD例2如右图示，平行四边形ABCD的两条对角线相交于点M，且，用，表示、、和.ABa�ADb�abMA�MB�MC�MD�分析:因为ABCD为平行四边形可知M为AC与BD的中点.所以MBMD�MCMA�12MCAC�12MBDB�ACABADab�DBABADab�解:在平行四边形ABCD中ACABADab�DBABADab�121()2MCACab�121()2MBDBab�MAMC�MDMB�又1()2MAab�1()2MDab�说明:我们在做有关向量的题型时,要先找清楚未知向量和已知向量间的关系,认真分析未知与已知之间的相关联系,从而使问题简化.baMCABD例3如右图,、不共线，,用、表示.OA�OB�()APtABtR�OA�OB�OP�OAPB分析：求，由图可知OP�OPOAAP�APtAB�OAtAB�ABOBOA�而解：APtAB�OPOAAP�(1)tOAtOB�说明：同上题一样，我们要找到与未知相...