高中数学 三角函数复习课件 北师大版必修4 课件VIP免费

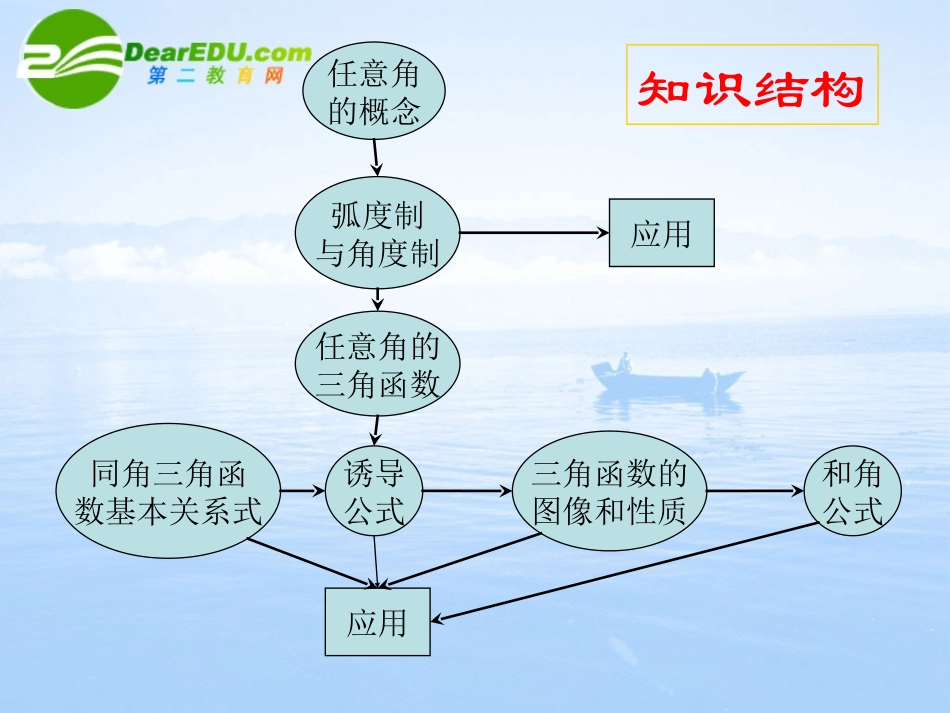
三角函数同角三角函数基本关系式和角公式三角函数的图像和性质诱导公式任意角的三角函数弧度制与角度制任意角的概念应用应用知识结构1、任意角的三角函数：xysincos=tan=rxyr角的终边上的任意一点p的坐标是x,y,它与原点的距离为rr>02、弧度制定义1弧度：在单元位圆中长为1个单位长度的弧所对的圆心角lR3、诱导公式(1)组2,2,,k的正弦、余弦、正切函数：函数名不变，符号看象限。(2)组3,22的正弦、余弦、：正余互化，符号象限。xyoP正弦线MA4.三角函数线:正弦线:余弦线:正切线:MPOMTAT正切线余弦线专题一、三角函数的概念专题训练：例1：如果是第一象限角，判断是第几象限角？22、)0452注：(1)应用象限角的概念判断(2错解:是第一象限角0<<902例、如果为第二象角，sincos试判断的符号cossin注：突破“单一按角度制思考三角问题”的习惯sin2131,2例、已知:则是第几象限角？3.已知coscosA.)(,sinsin是第一象限角，则、若下列命题成立的是tantan.coscos.tantan.是第四象限角，则、若是第三象限角，则、若是第二象限角，则、若DCB答案：D5、两角和与差的公式sin()sincoscossincoscoscossinsintantantan1tantan6、倍角公式22222sin22sincoscos2cossin2cos1=1-2sin2tantan21(tan)a7、半角公式1cos1cossincos22221cossin1costan21cos1cossin8、积化和差公式：1sincossinsin21cossinsinsin21coscoscoscos21sinsincoscos29、和差化积公式：sinsin2sin22sinsin2cossin22coscos2coscos22coscos2sinsin22cos注：左边是同名函数的和与差10、同角三角函数的基本关系22coscotsincos1倒数关系：tancot=1sin商数关系：tan=cos平方关系：sin专题二：同角三角函数基本关系2221sincossin2sinsincos4cos2例、已知tan=3，求式子4cos的值.关键：弦切22sincos2sincossincos(3)sin2cos11、已知tan=2,求值：1练习：注：公式的正用、反用、变形、“1”的变通。1例2、已知sin+cos=，50,,求cot的值注：在应用三角公式进行开方运算时，要根据角的范围，确定正负号的取舍。1332、已知sin+cos=，0,,3求sincos及sin+cos的值。练习：小结：三个式子中，已知其中一个式子的值，可以求出其余两个式子的值。sincos,sincos,sincos2233、已知0,,且sin,cos12是方程5x-x-=0的两个根，求5sin+cos、tan+cot以及tan-cot的值3,m-34-2m例、若sin=，cos=,m+5m+5,则m的取值范围？2注：不能单从角的范围考虑，而怱略了内在联系22sincos1专题三：三角函数求值1.例、设tan=5,tan-=4，4求tan+4,270,44练习1、已知cos-=-,cos=,5590<-<180<<360求cos2一、已知三角函数值求三角函数值2122、设cos-=-,sin=,293且<<,0<<,求cos的值2213、已知tan=-1,tan=，2sin2求的值sin2注：求某个三角函数值，关鍵是寻找所求角与已知角的联系。41例、已知、为锐角，且cos=，711cos=-,求的值。14注：求某个角，一般先求出这个角的某个三角函数值，即恰当选择三角函数（1）如果所求角的范围在第一、二象限则选则...