高中数学 23(向量的坐标表示和空间向量)课件 北师大版选修2-1 课件VIP免费

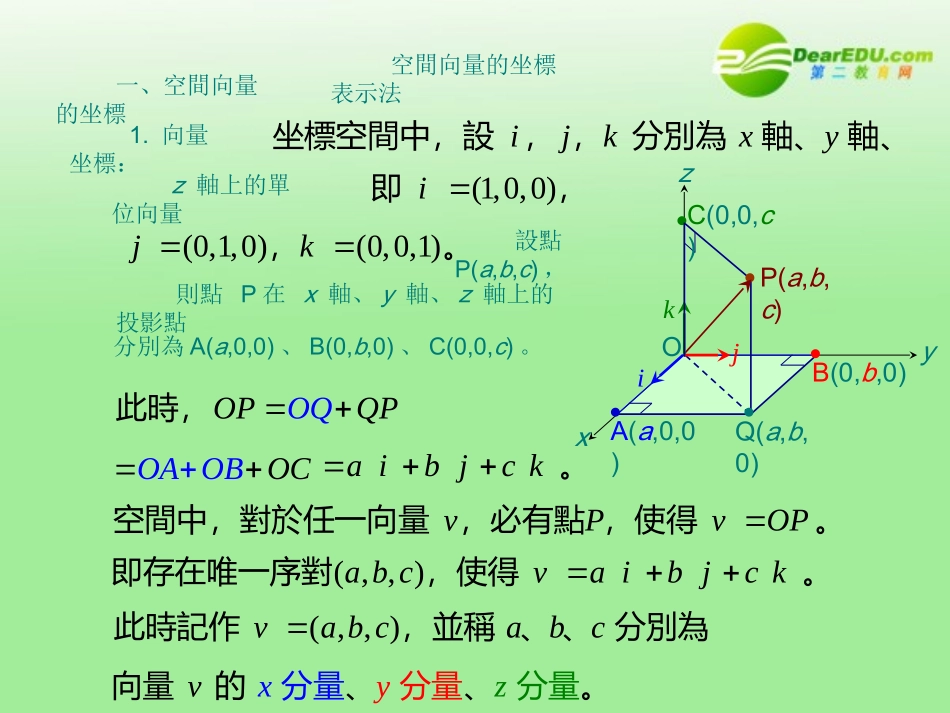
数学：２．３《向量的坐标表示和空间向量》课件PPT（北师大版选修2-1）iA(a,0,0)B(0,b,0)ijkxy坐標空間中，設，，分別為軸、軸、(0,1,0)(0,0,1)jk，。OQQOPP此時，OAOBOCaibjck。vPvOP空間中，對於任一向量，必有點，使得。(,,)abcvaibjck即存在唯一序對，使得。(,,)vabcabc此時記作，並稱、、分別為OxyzP(a,b,c)C(0,0,c)Q(a,b,0)jk空間向量的坐標表示法則點P在x軸、y軸、z軸上的投影點分別為A(a,0,0)、B(0,b,0)、C(0,0,c)。一、空間向量的坐標1.向量坐標：z軸上的單位向量xzvy向量的、量分量、分分量。(1,0,0)i即，設點P(a,b,c)，212211,,(),(),PxyzQxyz若，為坐標空間中兩點，111111),,(Pxyzxyzijk，222222),,(Qxyzxyzijk，OQOPPQ222111()()xiyjzxyjzkki121212()()()xyxyzijkz221112(,,)xxyyzz。121212(),,,),(QxPyyxzz若，，Oxyz111(,,)Pxyz222(,,)Qxyz說明：注意：221211(,,)PQxyxyzz則。22122221()()()PQQxyPxyzz則。222(,,)vabcvvabc設向量向量的長度。111222(,,)(,,)uxyzvxyz已知，，121212,,uvxxyyzz則。(,,)CDyzBDxA設，因為，A(1,2,3)B(4,3,1)C(2,–3,5)D(x,y,z)2.向量的長度：3.向量的相等：4.範例：空間坐標中，平行四邊形ABCD中，A(1,2,3)，解：B(4,3,1)，C(2,–3,5)，求D點坐標。則(x1,y2,z3)=(2,6,4)x=1，y=4，z=7。故D(1,4,7)。AByz求在平面上的正射影長。(6,4,3)AB(0,4,3)AByzu在平面上的正射影為。2220(4)35u故所求為。PQzx求在平面上的正射影長。(5,8,12)PQ(5,0,12)PQzxu在平面上的正射影為。222501213u故所求為。5.範例：空間坐標中，A(2,1,5)，B(8,3,2)，解：馬上練習：空間坐標中，P(2,4,3)，Q(7,4,9)，Ans：13。解：QRxyyzzx設在、、平面的正射影長分別為(,,)QRxyzQRxyyzzx設，則在、、平面的正射影(,,0),(0,,),(,0,)uxyvyzwxz分別為，2222uxy，223vyz，224wxz，2222()891633xyz解得：222336622QRxyz。6.範例：解：2234QR、、，求的長。10PQPQxyyz設，且在、平面的正射影長98PQzx分別為、，求在平面的正射影長。55。(,,)PQxyzPQxyyzzx設，則在、、平面的正射影(,,0),(0,,),(,0,)uxyvyzkxz分別為，229uxy，228vyz，22210(10)xyzPQ又222364519xyz解得：，，，22xz所求361955。馬上練習：Ans：解：11112222(,,)(,,)rvxyzvxyz設為實數，若，，12121212(1)(,,)vvxxyyzz；11112222()()vvxiyjzxyjzkki212121()()()xyxyzijkz112221(,,)xxyyzz。11112222()()vvxiyjzxyjzkki212121()()()xyxyzijkz112221(,,)xxyyzz。7.向量的坐標運算：證明：12121212(,,)vvxxyyzz。1111(2)(,,)rvrxryrz。1111()vxizkryrj111xiyjzrrkr111(,,)xyrrzr。證明：3420DADBDC且滿足，3(1,6,)4(3,1,2)xyzxyz33124820183448203841020xxxyyyzzz(,,)(7,30,18)xyz。8.範例：令A(1,6,0)，B(3,1,2)，C(4,4,5)為坐標空間中三點，若D為空間中一點，解：令D(x,y,z)2(4,4,5)(0,0,0)xyz求點D的坐標。11112222(,,)(,,)rvxyzvxyz設為實數，若，，111222122220//xyzxyzvvxyz且，則。2121//ttvvvv，為實數。212112(,,)(,,)xyzxytz221112ttxyxzzty，，221121xytzxyz。9.向量的平行：證明：(1)(1,3,5)(4,4,2)23ababab...