高中数学 21(函数的概念和图象)课件六 苏教版必修1 课件VIP免费

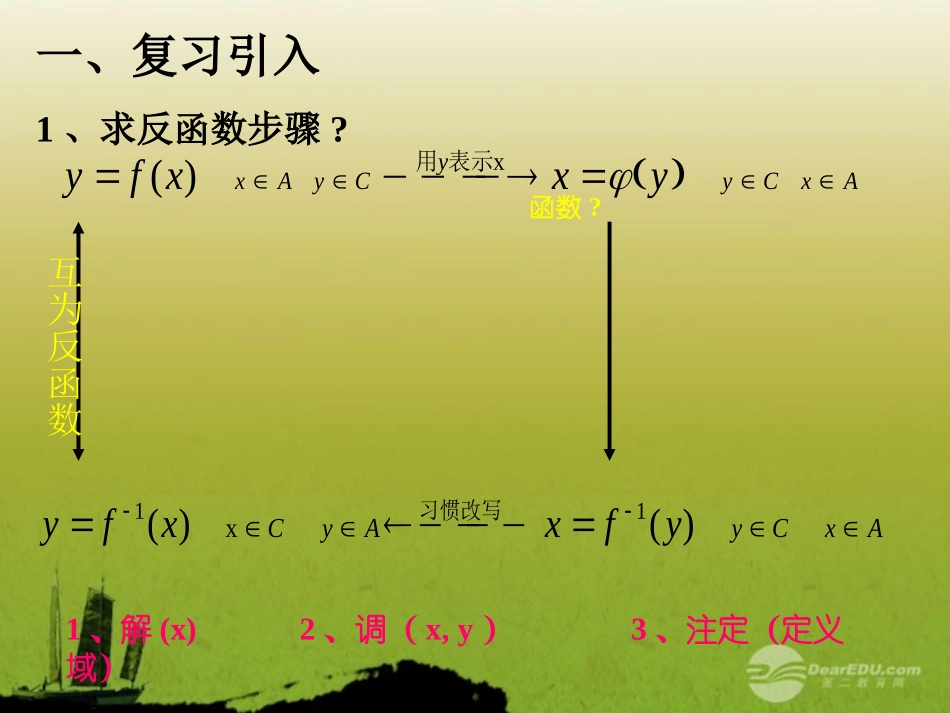
互为反函数的函数图象间的关系一、复习引入1、求反函数步骤?函数?AxCyyCyAxyxxfyx)(表示用AxCyAyCyfxxfy)()(11x习惯改写互为反函数1、解(x)2、调（x,y）3、注定（定义域）解:没有;因为它不是一一映射构成的函数；把定义域改写为(-∞,0]、[0,+∞)时它有反函数.2、函数y=2x2-3(xR)∈有没有反函数？为什么？如何改写定义域才能使其有反函数？012341234●P(2,4)●Q(4,2)xy-1-1y=x二、探索研究ABO’1、阅读课本，完成P63页第5题：（教材原题如下）•（1）在直角坐标系内，画出直线y＝x，然后找出下面这些点关于直线y＝x对称的点，并且写出它们的坐标（不必说明理由）：A（2，3），B（I，0），C（－2，－I），D（0，－l）A1（），B1（），C1（），D1（）．•（2）由上面各对称点的坐标之间关系可得出一般结论：点P（a，b）关于直线y＝x对称的点P’的坐标是（）．CyAxxfy)(AyCxfyx)(1互为反函数结论推广：任意点P(a,b)在原函数图象上即b=f(a)则点Q（b,a）在反函数图象上这个结论说明:原函数图象与反函数图象关于直线y=x对称。自学例1求函数y=3x-2(xR)∈的反函数，并且画出原来的函数和它的反函数的图象。解∵y=3x-2函数y=3x-2(xR)∈的反函数为y=32xx0y-2032x-20y0∴x=32y321-2-11-1-2xyy=3x-232xyxy函数y=f(x)的图象和它的反函数y=f-1(x)的图象关于直线y=x对称。注:这一结论是在坐标系中横轴为X轴，纵轴为y轴，而且横轴和纵轴的长度单位一致的前提下得出的．函数y＝f（x）的图象和它的反函数y＝f-1（x）的图象关于直线y＝x对称，而不是函数y＝f（x）与x＝f﹣1（y）的图象关于直线y=x对称．注意x0123…y0149…x0149…y0123…xyxyxyxyxy2xy2xy好画吗?怎样转化,用我们学过的知识来画?先画y=x2(x[0,+∞))∈这个我们熟悉!练习：①画出函数y=√x(x∈[0,+∞))的图象..,),()23(321)(2的值求也在反函数图象上在原函数图象上且点有反函数已知函数例ba，，ba，xxxf、)1(23)1()23(3212yyxxxy得由)1(23)1()(21xxxf原函数的反函数是32123)1(2abab.),(也在反函数的图象上既在原函数图象上点又，ba2,2ba解法一：因为点（a,b）在y=f(x)的反函数的图象上，所以点（b,a）在y=f(x)的图象上。321321baab所以a=2,b=2解法二：331)2(214)1(6xRxxyRxxy：，、且图象并画出函数及其反函的求下列函数的反函数练习:作业: