高中数学 9 演绎推理课件 理 新人教A版选修2-2 课件VIP免费

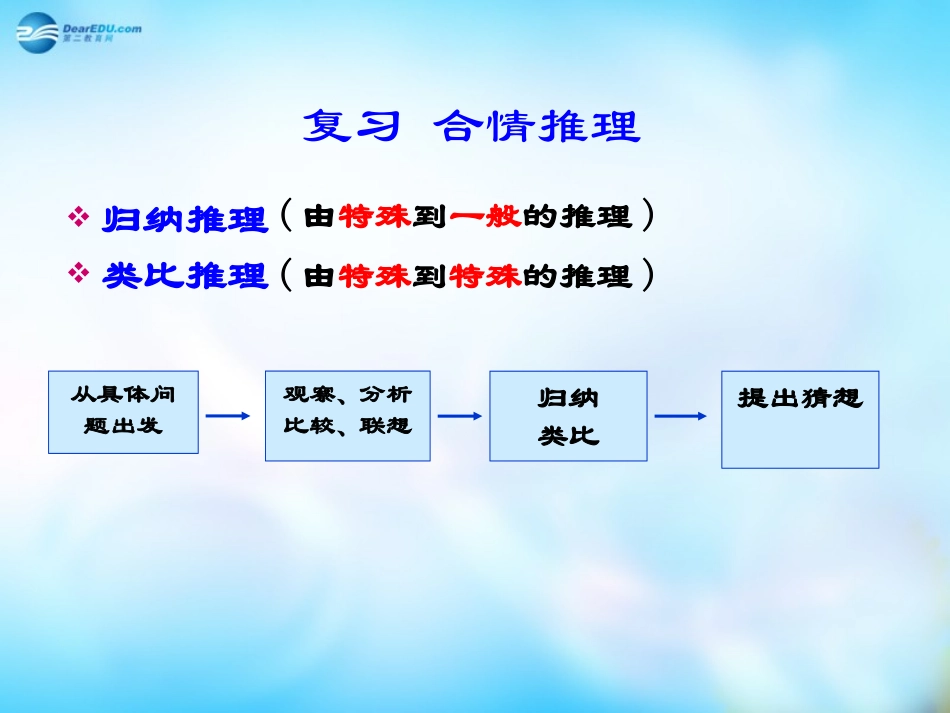
2.1.2演绎推理复习合情推理归纳推理类比推理从具体问题出发观察、分析比较、联想提出猜想归纳类比(由特殊到一般的推理)(由特殊到特殊的推理)观察与是思考1.所有的金属都能导电,2.一切奇数都不能被2整除,3.三角函数都是周期函数,4.全等的三角形面积相等上面的推理都是从一般性的原理出发，推出某个特殊情况下的结论，我们把这种推理称为演绎推理．因为铜是金属,所以铜能导电.因为(2100+1)是奇数所以(2100+1)不能被2整除.因为tanβ是三角函数,所以tanβ是周期函数如果三角形ABC与三角形A1B1C1全等,那么三角形ABC与三角形A1B1C1面积相等.从一般性的原理出发，推出某个特殊情况下的结论，这种推理称为演绎推理．１．演绎推理是由一般到特殊的推理；２．“三段论”是演绎推理的一般模式；包括⑴大前提---已知的一般原理；⑵小前提---所研究的特殊情况；⑶结论---根据一般原理，对特殊情况做出的判断．演绎推理又称逻辑推理。它的特征是，当前提为真时，结论必然为真。（但要注意：当前提为假时，结论必然为假。）1.所有的金属都能导电,2.一切奇数都不能被2整除,3.三角函数都是周期函数,4.全等的三角形面积相等所以铜能够导电.因为铜是金属,所以(2100+1)不能被2整除.因为(2100+1)是奇数,所以是tan周期函数因为tan三角函数,那么三角形ABC与三角形A1B1C1面积相等.如果三角形ABC与三角形A1B1C1全等,大前提小前提结论大前提小前提结论大前提小前提结论大前提小前提结论4.三段论推理的依据,用集合的观点来理解:若集合M的所有元素都具有性质P,S是M的一个子集,那么S中所有元素也都具有性质P.MS3.三段论可以表示为大前提：M是P小前提：S是M结论：S是P例.如图;在锐角三角形ABC中,AD⊥BC,BE⊥AC,D,E是垂足,求证AB的中点M到D,E的距离相等..ADECMB(1)因为有一个内角是直角的三角形是直角三角形,在△ABC中,AD⊥BC,即∠ADB=900所以△ABD是直角三角形同理△ABE是直角三角形(2)因为直角三角形斜边上的中线等于斜边的一半,M是Rt△ABD斜边AB的中点,DM是斜边上的中线所以DM=AB12同理EM=AB12所以DM=EM大前提小前提结论大前提小前提结论证明:应用三段论解题时，首先应该明确什么是大前提和小前提，但为了叙述简洁，如果大前提是显然的，则可以省略。P80例题6为什么？）推理的结论正确吗？（吗？）上面的推理形式正确（结论是增函数。所以小前提是指数函数，而大前提是增函数，因为指数函数212121xxxyyay的结论是错误的。是减函数），所以所得）＜＜（因为指数函数，但大前提是错误的（上面的推理的形式正确10aayx在演绎推理中，只要前提和推理形式是正确的，结论必定是正确的。111(0))(0)(0)nnnnnnnnnnaqqnNaaacqqqacqacqcqa证明：若（，则是等比数列通项公式为的数列是等比数列。大前提小前提结论是等比数列的数列式为用三段论证明：通项公nnnacqcqa)0(.23如图，在△ABC中，AC＞BC，CD是AB边上的高，求证：∠ACD＞∠BCDCBAD证明：在△ABC中，因为CD⊥AB，AC＞BC所以AD＞BD，于是∠ACD＞∠BCD。指出上面证明过程中的错误。222102z250xpxzp已知实数满足不等式＜，试判断方程有无实数根，并给出证明。无实数根方程＜＜＜，＜－＜－（＝的根的判别式方程＜－＜－，＜－＜，解得－＜解：由052z0441212)44052z2122120212222222pzppppzpxxx练习：4演绎推理是证明数学结论、建立数学体系的重要思维过程.但数学结论、证明思路的发现,主要靠合情推理。因此，我们不仅要学会证明，也要学会猜想。合情推理与演绎推理的区别与联系:•从推理的结论来看,合情推理的结论不一定正确,有待进一步证明;演绎推理在大前提、小前提和推理形式都正确的前提下，得到的结论一定正确.①归纳推理是由特殊到一般的推理;②类比推理是由特殊到特殊的推理;③演绎推理是由一般到特殊的推理.推理合情推理（或然性推理）演绎推理（必然性推理）归纳(特殊到一般）类比（特殊到特殊）三段论（一般到特殊）小结作业：P84A组6B组1