高中数学：31(空间向量的数量积)江苏课件(苏教版选修2-1) 课件VIP免费

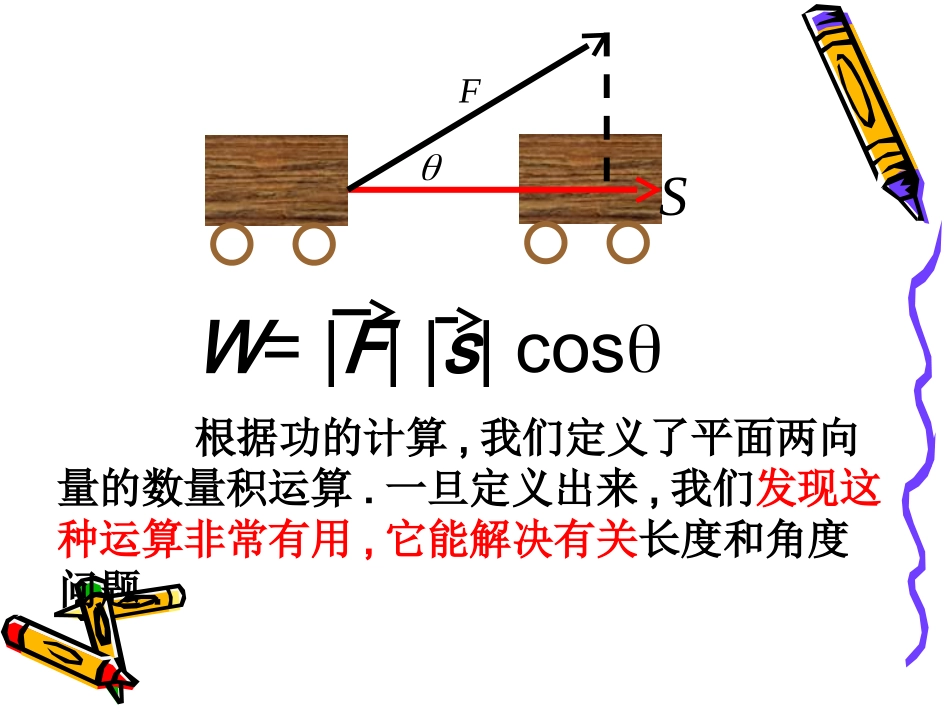
空间向量的数量积运算S�F�W=|F||s|cos根据功的计算,我们定义了平面两向量的数量积运算.一旦定义出来,我们发现这种运算非常有用,它能解决有关长度和角度问题.类似地,我们可以定义空间向量的数量积运算:1)两个向量的夹角的定义:OABaabb如图,已知空间两个非零向量、ab,在空间任取一点O,作OAa�,OBb�,则角AOB叫做向量a与b的夹角,记作:,ab.⑴规定:0,ab≤≤⑷如果,2ab,则称a与b垂直,记为ab,,abba这样规两个夹＝(2)在的定下，向量的角就被唯一确定了，并且⑶,ab=0时,ab与同向;,ab=π时,ab与反向2）两个向量的数量积已知空间两个非零向量、ab,则cos,abab叫做、ab的数量积,记作ab即cos,ababab.注:①两个向量的数量积是数量，而不是向量.②规定:零向量与任意向量的数量积等于零.③、仍是、的模。abab注:性质②是证明两向量垂直的依据；性质③是求向量的长度（模）的依据；注:性质②是证明两向量垂直的依据；性质③是求向量的长度（模）的依据；显然,对于非零向量、ab,e是单位向量有下列性质:①cos,aeaae；②0;abab③2aaa也就是说2aa.(3)空间两个向量的数量积性质(4)空间向量的数量积满足的运算律⑴()()abab⑵abba(交换律)⑶()abcabac(分配律)注意：数量积不满足结合律即)()abcabc（另外¿abacbc及000¿abab或这些运算律成立,说明数量积不仅有用,而且运算起来还极为方便课堂练习222222)()()()3)()()4)()abcabcpqpqpqpqpq��1.222,,22abab已知,则ab与的夹角大小为_____.2.判断真假:1)若0,ab则0,0ab()1352变：若呢？abADFCBE1(2)(3)(4)��图间边条边对线长点别点计（）3.如：已知空四形的每和角都等于1，、分是、的中。算：ABCDEFABADEFBAEFBDEFDCEFACD'C'B'DABCA'解：ACABADAA�22222222||()||||||2()4352(0107.5)85ACABADAAABADAAABADABAAADAA���||85AC�4435ABCDABCDABADAABADBAADAA00、已知在平行六面体中，，，，=90,==60，AC求对角线的长度。练习巩固:1.设a,b,c是任意的非零空间向量,且相互不共线,则：①(a·b)c(c·a)b=0②|a|-|b|<|ab|③(b·c)a(c·a)b不与c垂直④(3a+2b)·(3a2b)=9|a|2-4b2中,真命题是()(A)①②(B)②③(C)③④(D)②④2.已知向量,ab��满足1,2,3abab��,则ab��_____.4.如图，在空间四边形ABCD中，2AB，3BC，23BD，3CD，30ABD，60ABC，求AB与CD的夹角的余弦值奎屯王新敞新疆D1ABCD3.已知线段AB、BD在平面内,BDAB,⊥线段AC⊥,如果AB＝a,BD＝b,AC＝c,求C、D间的距离.222abc第3题:12第4题:法一:发现22222()ababab��代入求得.2.已知向量,ab��满足1,2,3abab��,则ab��_____.1法二:由2222abaabb��代入求得ab��=-2.∴2222abaabb��得ab��1法三:数形结合法,发现形的特殊性.妙!3.已知线段、在平面内，，线段如果，求、之间的距离.ABBDBDABAC,,ABaBDbACcCDcabCABD解： 22222222||()||||||CDCAABBDCAABBDabc��222CDabc复习：空间两个非零向量ab、的数量积ab:cos,ababab①22||aa即2||aa(求线段的长度);②ab0ab(垂直的判断);③cos,ababab(求角度).以上结论说明,可以从向量角度有效地分析有关垂直、长度、角度等问题.也有下列三个重要性质：abab,ab解： CD...