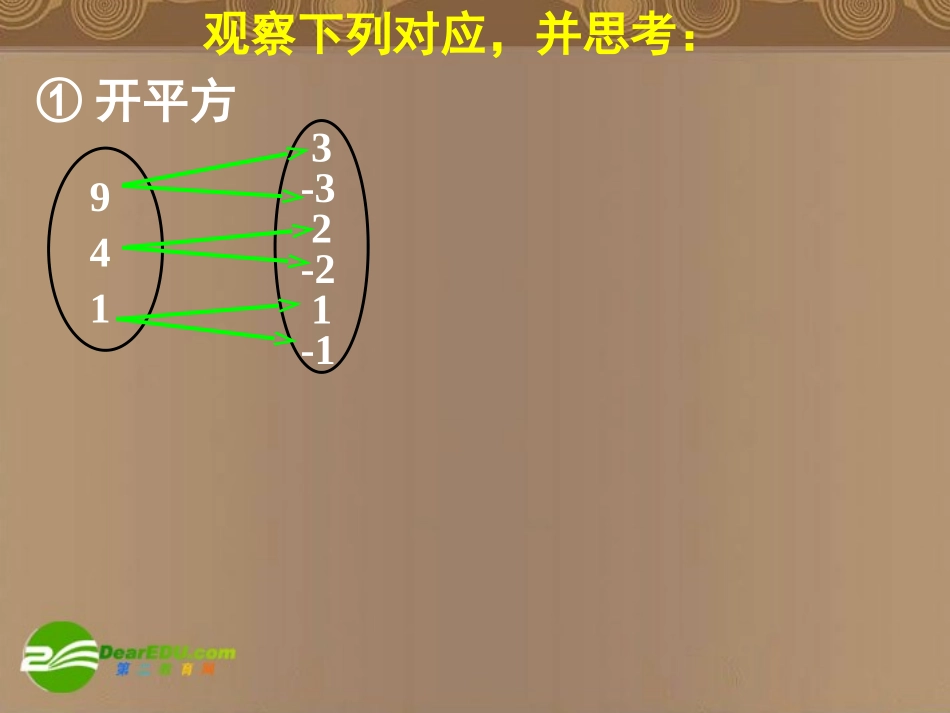
观察下列对应,并思考:讲授新课①开平方观察下列对应,并思考:9413-32-21-1①开平方1-12-23-3149②求平方观察下列对应,并思考:9413-32-21-1①开平方③求正弦1-12-23-3149②求平方观察下列对应,并思考:9413-32-21-1906045301232221①开平方③求正弦906045301232221④乘以21231234561-12-23-3149②求平方观察下列对应,并思考:9413-32-21-1一般地,设A、B是两个集合,如果按照某种对应法则f,对于集合A中的任一个元素,在集合B中都有唯一的元素和它对应,那么这样的对应(包括A、B以及A到B的对应法则f)叫做集合A到集合B的一个映射.映射的定义:一种对应是映射,必须满足两个条件:理解:一种对应是映射,必须满足两个条件:①A中任何一个元素在B中都有元素与之对应(至于B中元素是否在A中有元素对应不必考虑,即B中可有“多余”元素).理解:一种对应是映射,必须满足两个条件:①A中任何一个元素在B中都有元素与之对应(至于B中元素是否在A中有元素对应不必考虑,即B中可有“多余”元素).②B中所对应的元素是唯一的(即“一对多”不是映射,而“多对一”可构成映射,如图(1)中对应不是映射).理解:例1.判断下列对应是否映射?有没有对应法则?abcefgabcdefgabcefgd例1.判断下列对应是否映射?有没有对应法则?abcefgabcdefg是不是是1、3是映射,有对应法则,对应法则是用图形表示出来的.abcefgd例2.下列各组映射是否为同一映射?abcefgabcefgdbcefg下列对应关系(A到B)中,其中x∈A,y∈B..13:},104|{},31|{)5(;32:,,(4);:},1|{},10|{)3(;32:,,)2(;3:,)1(21xyxfyyBxxAxxyxfRBRAxyxfyyBxxAxyxfZBNAxyxfNBA其中构成映射的是.例3.(2)(4)(5)其中构成映射的是.下列对应关系(A到B)中,其中x∈A,y∈B.例3..13:},104|{},31|{)5(;32:,,(4);:},1|{},10|{)3(;32:,,)2(;3:,)1(21xyxfyyBxxAxxyxfRBRAxyxfyyBxxAxyxfZBNAxyxfNBA(1)集合A={P|P是数轴上的点},集合B=R,对应关系f:数轴上的点与它所代表的实数对应;(2)集合A={P|P是平面直角坐标系中的点},集合B={(x,y)|xR∈,yR}∈,对应关系f:平面直角坐标系中的点与它的坐标对应;例4.以下给出的对应是不是从集合A到B的映射?(3)集合A={x|x是三角形},集合B={x|x是圆},对应关系f:每一个三角形都对应它的内切圆;(4)集合A={x|x是新华中学的班级},集合B={x|x是新华中学的学生},对应关系f:每一个班级都对应班里的学生.例4.以下给出的对应是不是从集合A到B的映射?你能说出函数与映射之间的异同吗?思考:1)函数是一个特殊的映射;你能说出函数与映射之间的异同吗?思考:1)函数是一个特殊的映射;2)函数是非空数集A到非空数集B的映射,而对于映射,A和B不一定是数集.你能说出函数与映射之间的异同吗?思考:象与原象的定义:给定一个集合A到B的映射,且a∈A,b∈B,若a与b对应,则把元素b叫做a在B中的象,而a叫做b的原象.象与原象的定义:③求正弦906045301232221④乘以2123123456给定一个集合A到B的映射,且a∈A,b∈B,若a与b对应,则把元素b叫做a在B中的象,而a叫做b的原象.如图(3)中,此时象集C=B,但在(4)中,BC象与原象的定义:是的原象,是212130o的象,o30.给定一个集合A到B的映射,且a∈A,b∈B,若a与b对应,则把元素b叫做a在B中的象,而a叫做b的原象.练习:教材P.23第4题.中的元素是什么?相对应的素A22中元中的元素是什么?与相对应的中元素与的映射是“求正弦”,到,从,,是锐角设BBABABxxAo60)10(}|{例5.已知A=B=R,x∈A,y∈B,f:x→y=ax+b,若1,8的原象相应的是3和10,求5在f下的象.例6.已知A={1,2,3},B={0,1},写出A到B的所有映射.若f是从集合A到B的映射,如果对集合A中的不同元素在集合B中都有不同的象,并且B中每一个元素在A中都有原象,这样的映射叫做从集合A到集合B的一一映射.一一映射的定义:课堂小结(1)映射三要素:原象、象、对应法则;课堂小结(1)映射三要素:原象、象、对应法则;(2)取元任意性,成象唯一性;...