高中数学421直线与圆的位置关系课件人教版必修2 课件VIP免费

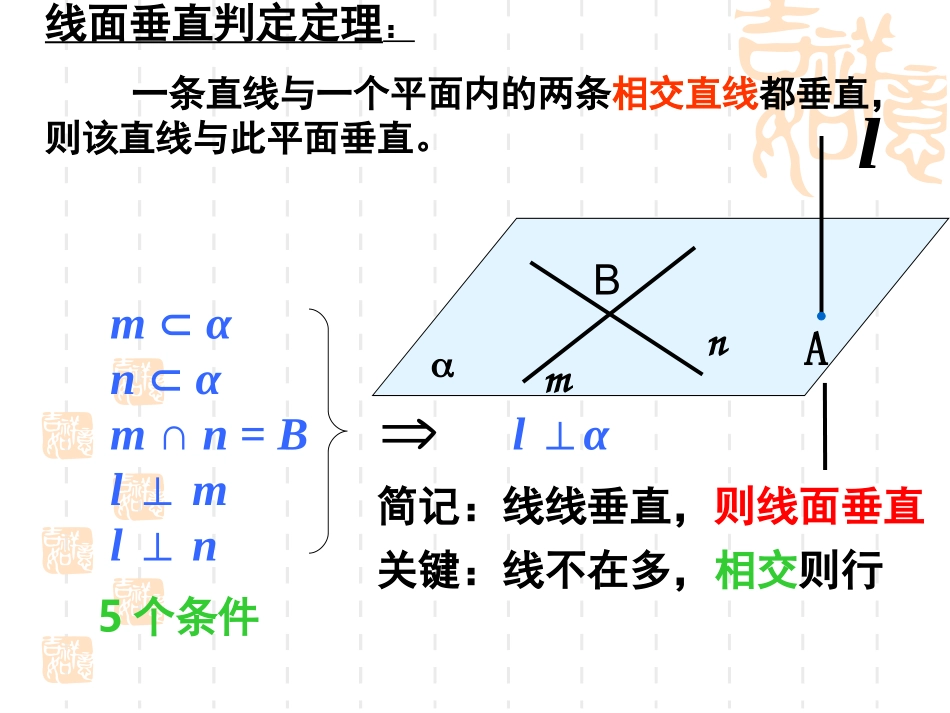
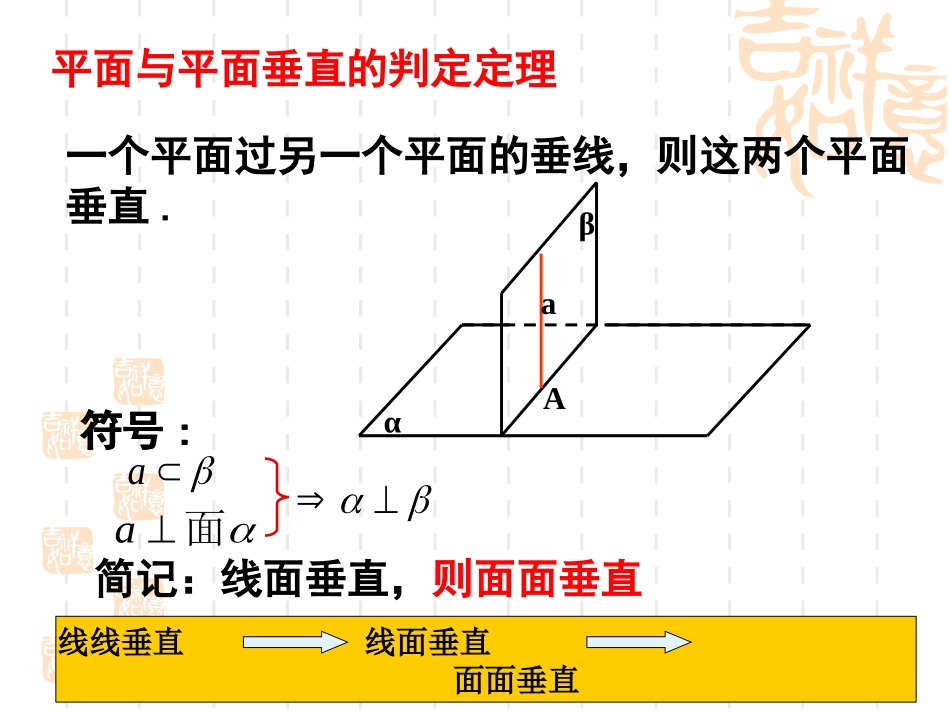
解析几何4.2.1直线与圆的位置关系线面垂直判定定理：一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直。mαnαm∩n=Bl⊥ml⊥nl⊥αAmnlB简记：线线垂直，则线面垂直关键：线不在多，相交则行5个条件平面与平面垂直的判定定理一个平面过另一个平面的垂线，则这两个平面垂直.符号:αβaA简记：线面垂直，则面面垂直面面垂直线面垂直线线垂直aa面符号:线面垂直的性质•线面垂直性质定理：垂直于同一个平面的两条直线平行。//aabbab//aabb//abab面面垂直的性质面面垂直性质定理：两个平面垂直，则一个平面内垂直于交线的直线与另一个平面垂直。面面垂直线面垂直αβaAllaalaACBDA1C1B1D1线面垂直正方体中包含了丰富的线面关系线面垂直关系——棱和侧面垂直ACBDA1C1B1D1111111111111111BCBCBCABBCABBBCABCDABABCD平面平面1111ABCDABCD平面平面11ABCD1BC平面111BCABCD平面ACBDA1C1B1D1线面垂直正方体中包含了丰富的线面关系线面垂直关系——对角线和对角面垂直ACBDA1C1B1D1线面垂直正方体中包含了丰富的线面关系线面垂直关系——对角线和对角面垂直ACBDA1C1B1D1线面垂直正方体中包含了丰富的线面关系线面垂直关系——对角线和对角面垂直ACBDA1C1B1D1线面垂直正方体中包含了丰富的线面关系线面垂直关系——对角线和对角面垂直ACBDA1C1B1D1线面垂直正方体中包含了丰富的线面关系线面垂直关系——对角线和对角面垂直作业讲评P134A2（2）解：设所求圆的方程为：因为A(-1,5),B(5,5),C(6,-2)都在圆上222222(-1)550555506(2)620DEFDEFDEF4220DEF22(2)(1)25xy即所求圆的方程为220xyDxEyF2242200xyxyP134A2（2）解：52756BCk设AB的中垂线的斜率为k1OAkk17kBC中点为113,22OA中垂线中垂线方程为3111()272yx联立两条直线方程3111()2722yxx21xy||5rOB半径21圆心，所求圆的方程为22(2)(2)25xyxyOEA(-1,5)B(5,5)C(6,-2)AB中点为（2，5）2(2,5)AB中垂线中垂线方程为x=2P137问题xyOBACD直线和圆的位置关系Cldr相交：rdCl相切：rdCl相离：rdd例1.已知直线与圆判断l与圆的位置关系:360lxy22240xyyxyOCBA解：几何法22240xyy22(1)5xy圆心（0，1）5r设C到直线l的距离为d0022||AxByCdAB22|3016|31d5105所以直线l与圆相交有两个公共点练习P140练习3用几何法dxOC解：几何法2220xyx22(1)1xy圆心（1，0）1r设C到直线l的距离为d0022||AxByCdAB22|3102|34d1r所以直线l与圆相切有一个公共点y例1.已知直线与圆判断l与圆的位置关系:360lxy22240xyyxyOCBA解：代数法22360240xyxyy联立圆和直线的方程得由①得36yx把上式代入②2320xx①②2(3)41(2)1④所以方程④有两个不相等的实根x1，x2把x1，x2代入方程③得到y1，y2③所以直线l与圆有两个不同的交点A(x1,y1),B(x2,y2)0练习P140练习4用代数法xyOC解：代数法226240yxxyy联立圆和直线的方程得把①代入②25100xx①②2(5)41(10)15所以方程③没有实数根③所以直线l与圆没有交点，它们相离。0例：以C(1,3)为圆心,并且和直线3x-4y-7=0相切的圆.圆心：已知半径：圆心到切线的距离解：设所求圆的半径为r则：2243|7-34-13|r=516∴所求圆的方程为：CyxOM22196(1)(3)25xy练习P140练习17r2249xy请同学们谈谈这节课学到了什么东西。学完一节课或一个内容，学完一节课或一个内容，应当及时应当及时小结小结，梳理知识，梳理知识小结：判断直线和圆的位置关系几何方法求圆心坐标及半径r（配方法）圆心到直线的距离d（点到直线距离公式）代数方法0)()(222CByAxrbyax消去y（或x）20pxqxt0:0:0:相交相切相离:::drdrdr相交相切相离作业A：小结B：P144A1