高中数学 第一章 三角函数 142 正、余弦函数的性质(一)课件 新人教A版必修4 课件VIP免费

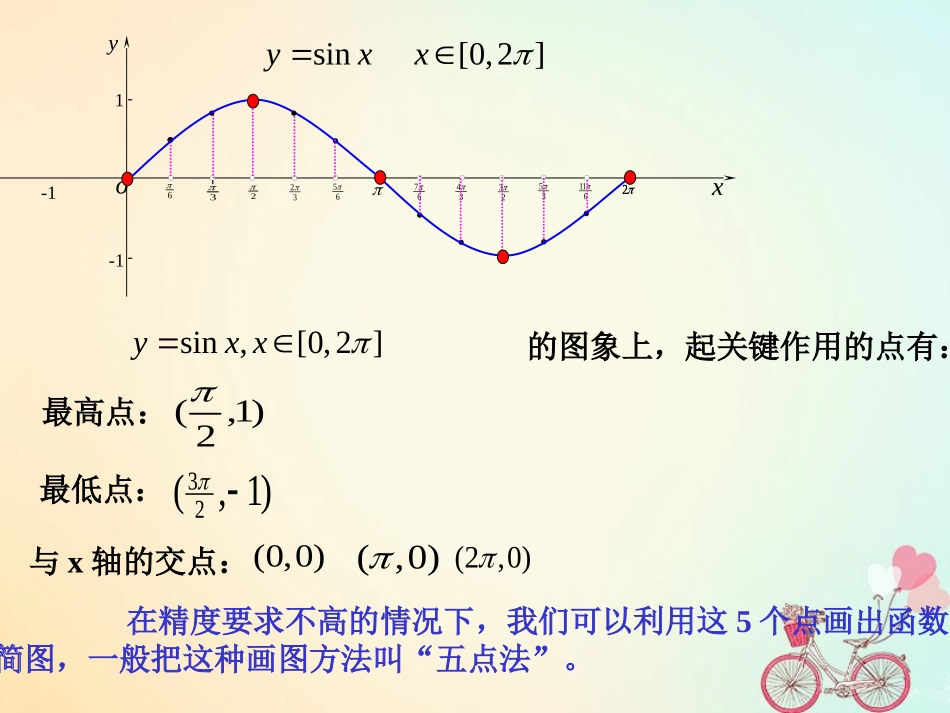
1.4.2正弦函数、余弦函数的性质（一）2oxy---11--13232656734233561126sin[0,2]yxx在函数的图象上，起关键作用的点有：sin,[0,2]yxx最高点：最低点：与x轴的交点：(0,0)(,0)(2,0))1,(23)1,2(在精度要求不高的情况下，我们可以利用这5个点画出函数的简图，一般把这种画图方法叫“五点法”。正弦曲线：余弦曲线：sinyxxRcosyxxRxy1-1xy1-1对于函数f(x)，如果存在一个非零常数T，使得当x取定义域内的每一个值时，都有f(x+T)=f(x)那么函数f(x)就叫做周期函数，非零常数T叫做这个函数的周期。如果在周期函数f(x)的所有周期中存在一个最小的正数，那么这个最小的正数就叫做f(x)的最小正周期。例如正弦函数是周期函数，2kπ（kZ,k≠0)∈都是它的周期，最小正周期是2kπ正弦曲线：sinyxxRxy1-1对称性：对称轴：,2xkkZ对称中心：(,0)kkZ奇偶性：奇函数sin(－x)=－sinx周期性：正弦函数是周期函数，都是它的周期，最小正周期是。2(,0)kkZk且2对称性：对称轴：,xkkZ对称中心：(,0)2kkZ奇偶性：偶函数cos(－x)=cosx周期性：余弦函数是周期函数，都是它的周期，最小正周期是。2(,0)kkZk且2余弦曲线：cosyxxRxy1-1例1.求下列函数的周期。3cos,sin2,12sin(),.26yxxRyxxRyxxR(1);(2);(3)例2.判断函数的奇偶性。1()sin()22fxxsin()yAx函数的周期是2cos()yAx函数的周期是2正弦曲线：sinyxxRxy1-1最值：22xk当时，max1y22xkmin1y当时，函数的最值：正弦曲线：sinyxxRxy1-1余弦曲线：cosyxxRxy1-1练习：P40T1、T2、T3作业：P52T2、T3练习：1.判断下列说法是否正确：（1）点是函数的图象上的一个最高点；（2）直线是函数的图象上的一条对称轴；（3）函数的图象关于y轴对称；（4）函数在间的图象与在间的图象形状相同；（5）点是函数的图象的一个对称点。3(,1)2sin,yxxR52xsin,yxxRcos,yxxRsin,yxxR[8,10][2,0](,0)2cos,yxxR