高中数学(解析几何)对称问题教学课件 苏教版必修2 课件VIP免费

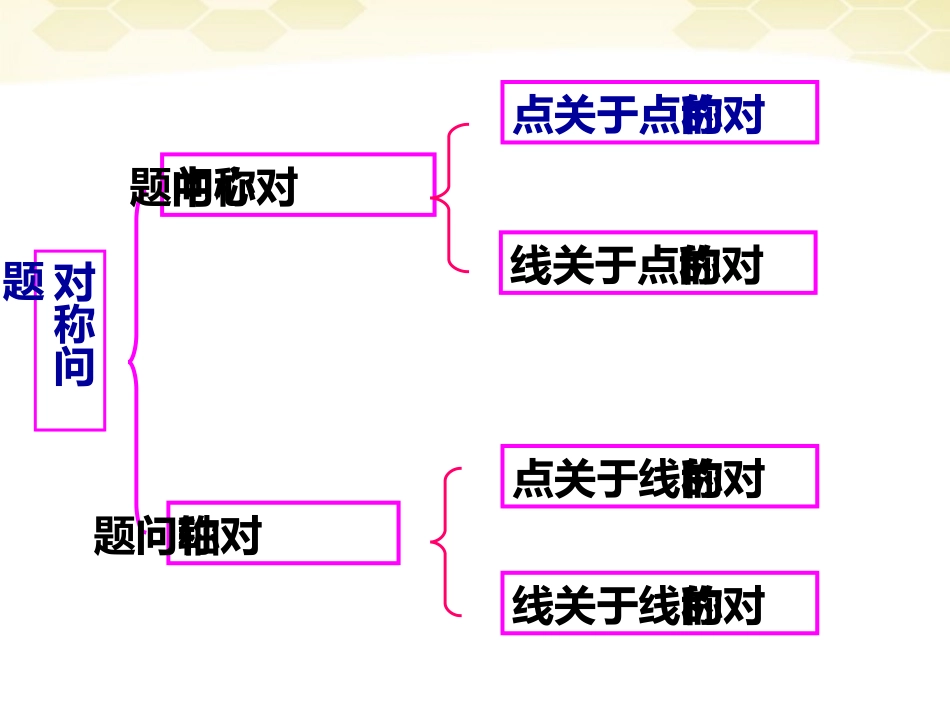
对称问题对称问题中心对称问题点关于点的对称线关于点的对称轴对称问题点关于线的对称线关于线的对称轴对称中心对称有一条对称轴:直线有一个对称中心:点定义沿轴翻转180°绕中心旋转180°翻转后重合旋转后重合性质1、两个图形是全等形2、对称轴是对应点连线的垂直平分线3、对称线段或延长线相交，交点在对称轴上1、两个图形是全等形2、对称点连线都经过对称中心，并且被对称中心平分。例1.已知点A(5,8)，B(4，1)，试求A点关于B点的对称点C的坐标。一、点关于点对称解题要点：中点公式的运用A(x0,y0)PP((aa,,bb))(2(2aa--xx00，，22bb--yy00))AA＇＇一般地，点A(x0,y0)关于点PP((aa,,bb))的对称的对称点是点是(2(2aa--xx00，，22bb--yy00))例2.求直线l1:3x-y-4=0关于点P(2,-1)对称的直线l2的方程。二、直线关于点对称法一：l2上的任意一点的对称点在l1上f(x,y)=0M(x,y)P(m,n)P(m,n)MM′′(2m-x,2n-y)(2m-x,2n-y)ff(2m-x,2n-y)=0(2m-x,2n-y)=0法二：l1//l2且P到两直线等距。例3.已知点M的坐标为(-4,4)，直线l的方程为3x+y-2=0,求点A关于直线l的对称点M′的坐标。三、点关于直线对称解题要点：k•kMM′=-1MM′中点在l上M(xM(x11,y,y11))MM′′(x,y)(x,y)l例4.试求直线l1:x-y-2=0关于直线l2:3x-y+3=0对称的直线l的方程。四、直线关于直线对称解题要点：由线关于线对称转化为点关于点对称思考：若l1//l2,如何求l1关于l2的对称直线方程？C1lC2M(x,y)M(x,y)MM＇＇(x(x11,y,y11))l1l2l1'几种特殊的对称：几种特殊的对称：①点P(x,y)关于下列点或线的对称点分别为：关于原点:__________;关于x轴:__________;关于y轴:__________;关于直线y=x:______;关于直线y=-x:______;关于直线x=a:_______.②直线f(x,y)=0关于下列点或直线对称的直线方程分别为：关于原点:____________;关于x轴:____________;关于y轴:___________;关于直线y=x:_________;关于直线y=-x:________;关于直线x=a:_________.(-x,-y)(x,-y)(-x,y)(y,x)(-y,-x)(2a-x,y)f(-x,-y)=0f(x,-y)=0f(-x,y)=0f(y,x)=0f(-y,-x)=0f(2a-x,y)=0设直线则关于轴对称的直线是＿＿＿＿＿＿＿关于轴对称的直线是＿＿＿＿＿＿＿＿关于对称的直线是＿＿＿＿＿＿＿关于对称的直线是＿＿＿＿＿＿llll0:CByAxlxyxyxy0)(CyBAx0)(CByxA0CAyBx0)()(CxByA轴对称应用例１：已知△ABC的顶点A（4,－1）,B（－4,－5）,角B的内角平分线BE所在直线的方程为，求BC边所在直线方程。01yxB(-4,-5)A(4,-1)M（0,3）xyOE解决三角形中的角平分线问题变式：△ABC的一个顶点是A（3，-1），∠B,C∠的内角平分线所在的直线方程分别为x=0和y=x,求顶点B、C坐标·。xyOxy0xA（3,-1）A1(-3,-1)A2(-1,3)B(0,5)C(-5,-5)y=2x+5例例22：一条光线经过点P（2，3），射到直线x+y+1=0上，反射后，穿过点Q（1，1），求光线的入射线和反射线的方程。xyOx+y+1=0P(2,3)Q(1,1)31,32SR(-4,-3))32(0245xyx)32(0154xyx解决物理光学方面的问题例3：光线从点P（－3，4）射出，到达x轴上的点Q后，被x轴反射到y轴上的点M，又被y轴反射，这时反射光线恰好经过点D（－1，6），求QM所在直线方程。xOP(-3,4)D(-1,6)yD′(1,6)P′(-3,-4)MQ例4：已知x,y满足x+y=0，求的最小值。2222)3()2()1()3(yxyx解决求最值的有关问题M′(1,-3)xyOM(3,-1)N(-2,3)y=－xP一、点关于点对称二、点关于直线对称三、直线关于点对称四、直线关于直线对称五、交点问题六、定点问题七、反射问题两条直线的位置关系------对称四类对称四类对称四类对称四类对称常见运用常见运用常见运用常见运用