高三数学 对一道数学题的研究性学习沪教版 学案VIP免费

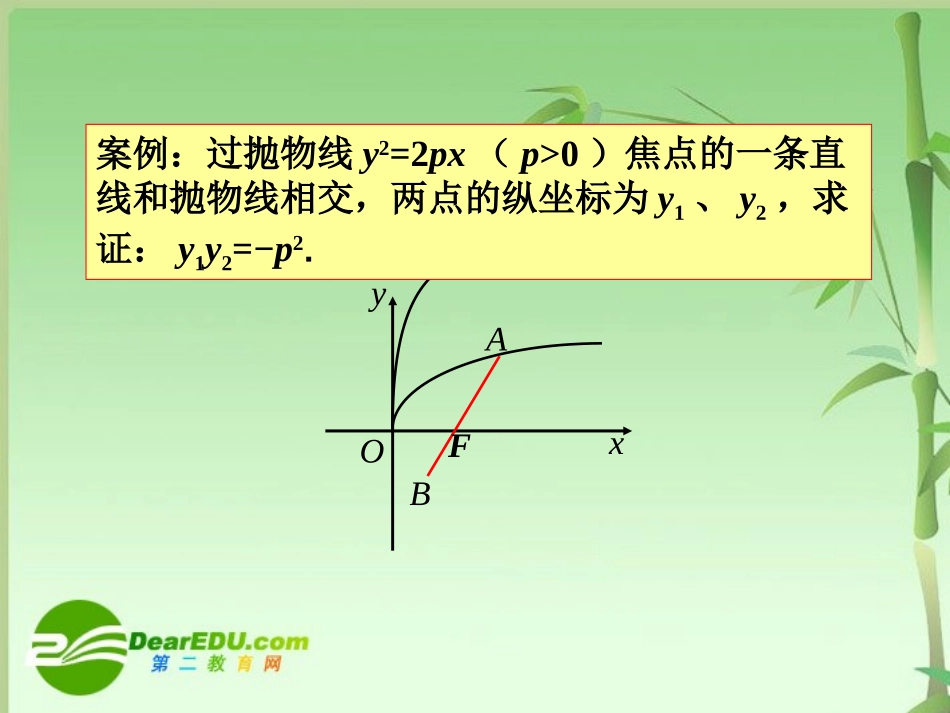
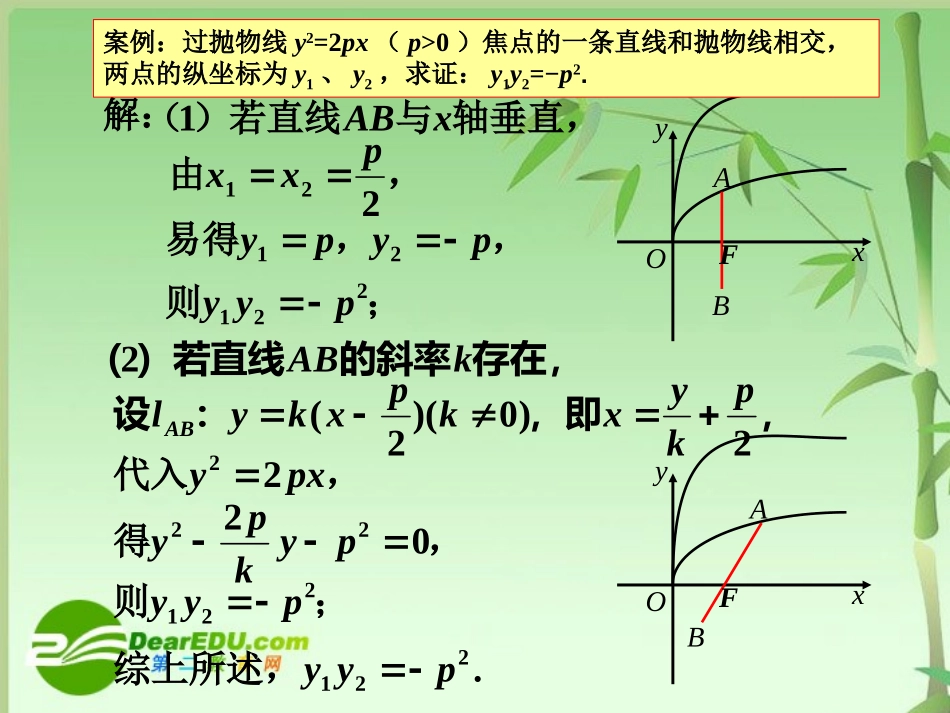
七宝中学授课教师：卜照泽yxOABF案例：过抛物线y2=2px（p>0）焦点的一条直线和抛物线相交，两点的纵坐标为y1、y2，求证：y1y2=−p2.解：轴垂直，与）若直线（xAB1，由221pxx，，易得pypy21；则221pyy存在，的斜率）若直线（kAB2，，即：设2)0)(2(pkyxkpxkylAB，代入pxy22，得0222pykpy.221pyy综上所述，；则221pyyyxOABFyxOABF案例：过抛物线y2=2px（p>0）焦点的一条直线和抛物线相交，两点的纵坐标为y1、y2，求证：y1y2=−p2.即：一条直线和抛物线y2=2px（p>0）相交，两交点的纵坐标为y1、y2，若y1y2=−p2，那么该直线过此抛物线的焦点吗？问题1.试问上题的逆命题是否成立？yxOAB解：的斜率不存在时，）若直线（AB1，则221pxx，，有pypy21；，过焦点即直线)02(pFAB存在，的斜率）若直线（kAB2，代入pxy22.02），（过焦点直线pFAByxOABFyxOABF一条直线和抛物线y2=2px（p>0）相交，两交点的纵坐标为y1、y2，若y1y2=−p2，那么该直线过此抛物线的焦点吗？，，即：设akyxkaxkylAB)0)(()2(pxkyAB：即直线，得0222paykpy，则2212ppayy，2pa如：一条直线和抛物线y2=2px（p>0）相交，两交点的纵坐标分别为y1、y2，若该直线过定点(c,0)(c>0)，那么y1y2是否为定值？yxOABP问题2.上题的条件推广以后，又如何呢？yxOABP解：轴垂直，与）若直线（xAB1，由cxx21，，易得pcypcy2221；则pcyy221存在，的斜率）若直线（kAB2，，即：设ckyxkcxkylAB)0)((，代入pxy22，得0222pcykpy.221pcyy综上所述，；则pcyy221yxOABP如：一条直线和抛物线y2=2px（p>0）相交，两交点的纵坐标分别为y1、y2，若该直线过定点(c,0)(c>0)，那么y1y2是否为定值？yxOABP问题3.一条直线和抛物线相交，两交点的纵坐标为，若，那么该直线过定点(,0)2vp22(0)ypxp12yy、12yyv问题4.若一条直线和抛物线y2=2px（p>0）相交，交于A、B两点，O为坐标原点，如果，那么直线AB过定点吗？0OAOB�yxOABE解：若一条直线和抛物线y2=2px（p>0）相交，交于A、B两点，O为坐标原点，如果，那么直线AB过定点吗？0OAOB�)0(1aaxABAB：线的斜率不存在，则设直）若（paypay2,221易得).02()2()1(，过定点知直线、所以，由pEAByxOABE0OAOB�，，02121yyxx2212122221404pyyyypyy，即pappa2,422即)0)((2kaxkykAB存在，则设的斜率）若（，代入pxy22yxOABEpxAB2:直线pappa2,422即)2(:pxkyAB直线，得0222paykpyyxOABE问题5.若一条直线和抛物线相交，交于A、B两点，O为坐标原点，如果直线AB过定点(2p，0)，则有成立。0OAOB�22(0)ypxp问题6.在抛物线y2=2px（p>0）中，过顶点O作两条直线交抛物线于A、B两点，且(c为定值)，连A，B交X轴于E点，则E点为定点.cOBOAyy,021yxOABE解：)0(:1aaxABAB线的斜率不存在，则设直）若（02)(2cpaa式，得代入paypay2,221易得yxOABE在抛物线y2=2px（p>0）中，过顶点O作两条直线交抛物线于A、B两点，且(c为定值)，连A，B交X轴于E点，则E点为定点.cOBOAyy,021),(22舍去或即cppacppa)0,0)((2akaxkykAB存在，则设的斜率）若（yxOABE,22pxy代入，COBOA，Cyyxx2121)(42122221，即cyypyy式整理得，代入)(221payy)(0222舍负，即cppacpaa.0,2）点为定点（cppE，得0222paykpy.0,2）点为定点（cppE在平面直角坐标系xoy中，直线l与抛物线相交于A、B两点。（1）求证:“如果直线l过点T(3,0)，那么”是真命题；（2）写出（1）命题的逆命题，判断它是真命题还是假命题，并说明理由。22yx3OAOB�2006年上海高考卷第20题问题7.若过抛物线y2=2px（p>0）上一点P（x0，y0），作两条直线使它们的斜率之积为定值，则另一条边所在的直线是否过定点？yxOABPE在数学的领域中，提出问题的艺术比解答问题的艺术更为重要。——康托尔数学的创作绝不是单靠推论可以得到的，首先通常是一些模...