高中数学 3.1.3空间向量的数量积运算课件 新人教A版选修2-1 课件VIP免费

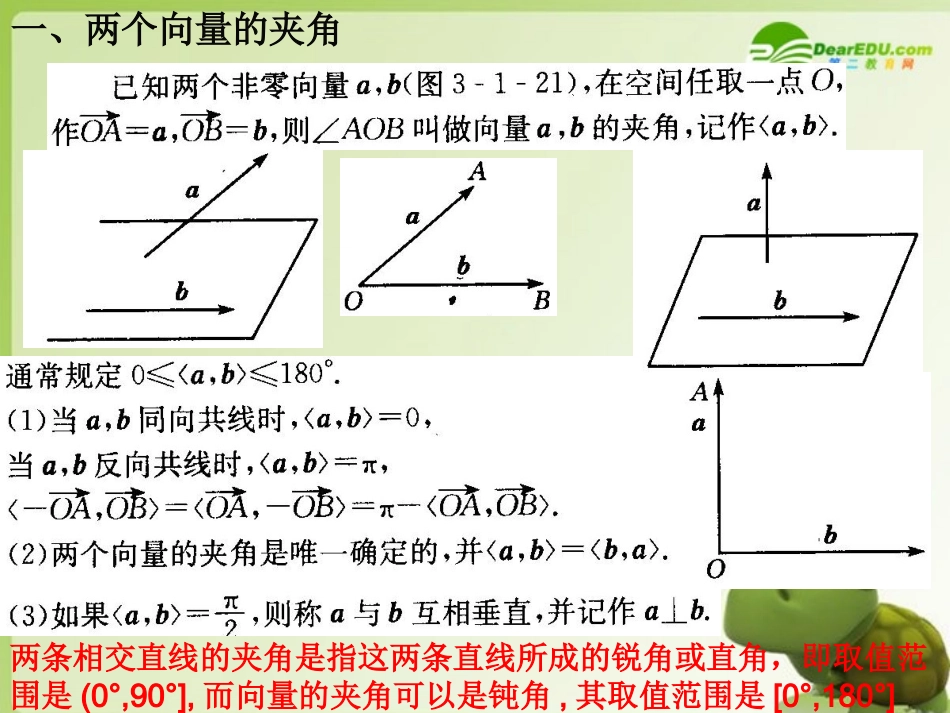
3.1.3空间向量的数量积运算一、两个向量的夹角两条相交直线的夹角是指这两条直线所成的锐角或直角，即取值范围是(0°,90°],而向量的夹角可以是钝角,其取值范围是[0°,180°]二、两个向量的数量积注:①两个向量的数量积是数量，而不是向量.②规定:零向量与任意向量的数量积等于零.abB类比平面向量,你能说出ab的几何意义吗?B1如图11AB�是b在a方向上的射影向量.AA1不一定为锐角不一定为钝角三、空间两个向量的数量积的性质(1)空间向量的数量积具有和平面向量的数量积完全相同的性质.(2)性质(2)是用来判断两个向量是否垂直，性质(5)是用来求两个向量的夹角．(3)性质(3)是实数与向量之间转化的依据．四、空间向量数量积的运算律与平面向量一样，空间向量的数量积满足如下运算律：向量数量积的运算适合乘法结合律吗?即(a•b)c一定等于a(b·c)吗?注意：数量积不满足结合律即)()abcabc（另外¿abacbc及000¿abab或已知空间向量a，b满足|a|=4，|b|=8，a与b的夹角是150°，计算：(1)(a+2b)·(2n-b)；(2)|4a一2b|．如图，已知空间四边形ABCD的每条边和对角线长都等于a，点E、F、G分别是AB、AD、DC的中点。求下列向量的数量积：(1);(2);(3);(4).ABACADBDGFACEFBC��练习1ABCDEFG在平行四边形ABCD中，AB=AC=1，∠ACD=90°，将它沿对角线AC折起，使AB与CD成60°角，求B，D间的距离．练习2练习3ABCDABCD4AB3,5,90,60ADAABADBAADAAACD'C'B'DABCA'解：ACABADAA�||85AC�22||()ACABADAA�222||||||2()ABADAAABADABAAADAA��2224352(0107.5)85已知空间四边形OABC中，M，N，P，Q分别为BC，AC，OA，OB的中点，若AB=OC，求证：PM⊥QN．证明：练习4练习5如图，在正三棱柱中，若，则与所成的角的大小为（）A.B.C.D.111ABCABC1AB1CB12ABBB06009001050756.如图，在空间四边形ABCD中，2AB，3BC，23BD，3CD，30ABD，60ABC，求AB与CD的夹角的余弦值奎屯王新敞新疆解：∵CDBDBC�，∴ABCDABBDABBC�||||cos,ABBDABBD�||||cos,ABBCABBC�223cos15023cos120633∴31cos,232||||ABCDABCDABCD���，∴AB与CD的夹角的余弦值为12．说明：由图形知向量的夹角时易出错，如,150ABBD�易错写成,30ABBD�，注意推敲！