高中数学 1.2应用举例(三)课件 新人教A版必修5 课件VIP免费

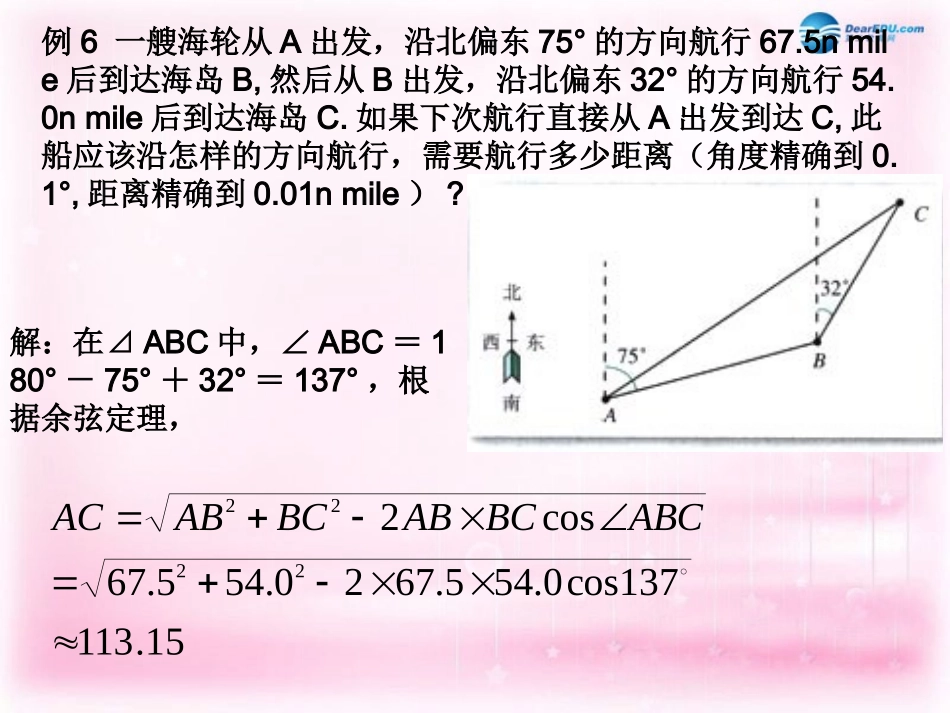
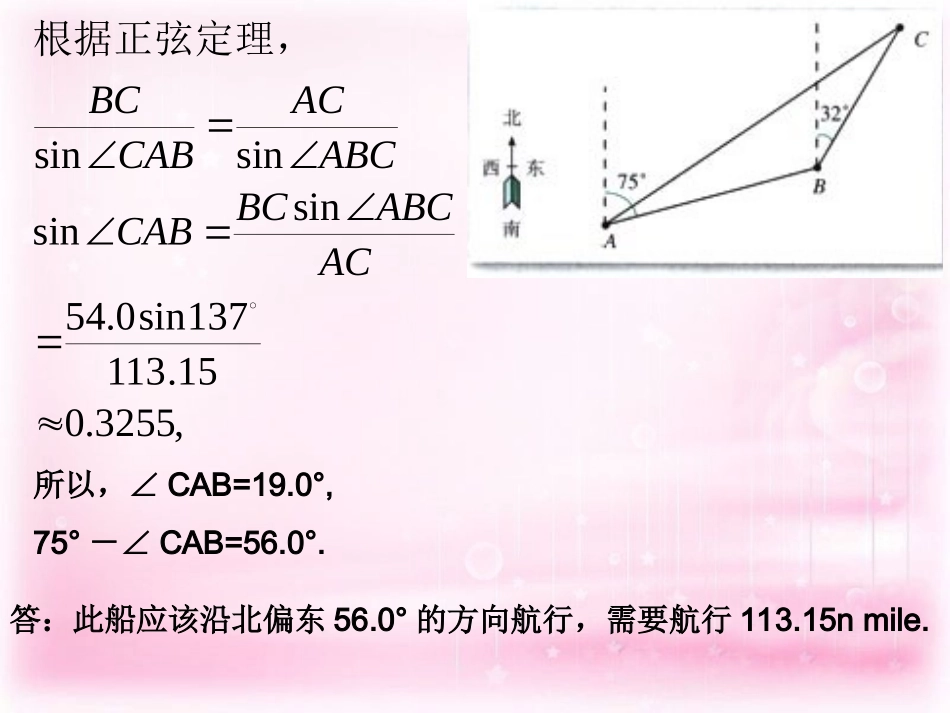
1.2应用举例（三）例6一艘海轮从A出发，沿北偏东75°的方向航行67.5nmile后到达海岛B,然后从B出发，沿北偏东32°的方向航行54.0nmile后到达海岛C.如果下次航行直接从A出发到达C,此船应该沿怎样的方向航行，需要航行多少距离（角度精确到0.1°,距离精确到0.01nmile）?解：在⊿ABC中，∠ABC＝180°－75°＋32°＝137°，根据余弦定理，15.113137cos0.545.6720.545.67cos22222ABCBCABBCABAC,3255.015.113137sin0.54sinsinsinsinACABCBCCABABCACCABBC根据正弦定理，所以，∠CAB=19.0°,75°－∠CAB=56.0°.答：此船应该沿北偏东56.0°的方向航行，需要航行113.15nmile.例7在⊿ABC中，根据下列条件，求三角形的面积S(精确到0.1cm²)(1)已知a=14.8cm,c=23.5cm,B=148.5°;)(9.905.148sin8.145.2321,sin21)1(2cmSBcaS得应用解：(2)已知B=62.7°,C=65.8°,b=3.16cm;).(0.47.62sin5.51sin8.65sin16.321,5.51)8.657.62(180)(180,sinsinsin21sin21,sinsin,sinsin)2(222cmSCBABACbAbcSBCbcCcBb根据正弦定理，（3）已知三边的长分别为a=41.4cm,b=27.3cm,c=38.7cm.).(4.5116384.04.417.3821,sin216384.07697.01cos1sin7679.04.417.3823.274.417.382cos3222222222cmSBcaSBBcabacB得应用，得）根据余弦定理的推论（例8在某市进行城市环境建设中，要把一个三角形的区域改造成市内公园，经过测量得到这个三角形区域的三条边长分别为68m,88m,127m，这个区域的面积是多少（精确到0.1cm²）?解：设a=68m,b=88m,c=127m,根据余弦定理的推论，.38.2840).(38.28406578.06812721,sin21.6578.07532.01sin,7532.068127288681272cos222222222mmSBcaSBcabacB答：这个区域的面积是得应用).coscoscos(22sinsinsin19222222222CabBcaAbccbaCBAcbaABC）（；）（中，求证：在例在任一中，求证：ABC0)sin(sin)sin(sin)sin(sinBAcACbCBa在⊿ABC中，若B=60°,2b=a+c,试判断⊿ABC的形状。