高一数学向量的数量积课件 人教版 课件VIP免费

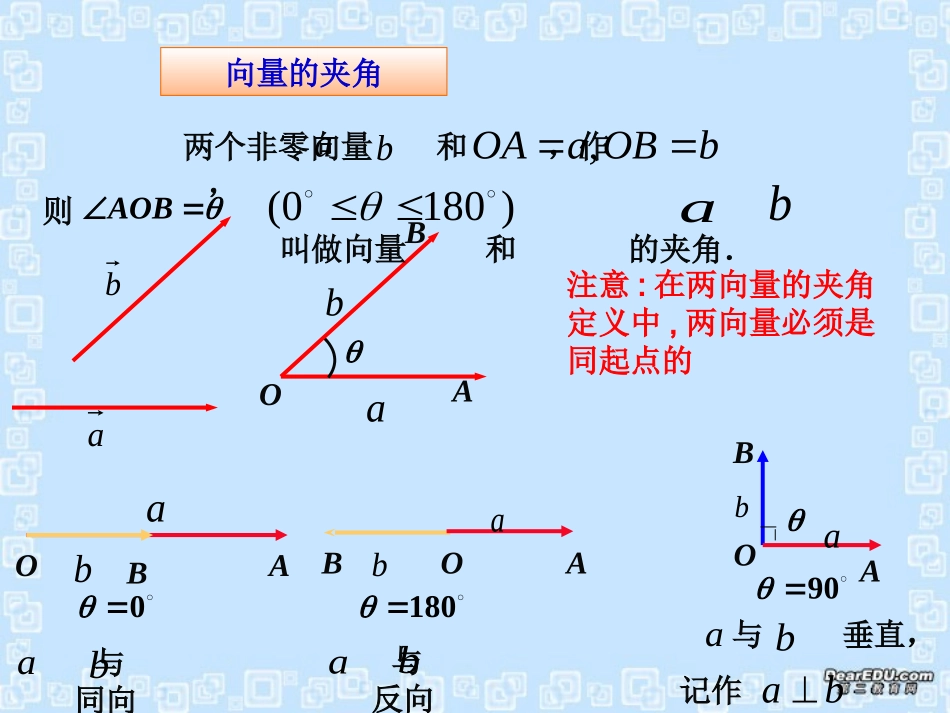
Fs┓问题θsF一个物体在力F的作用下产生的位移s，且F与s的夹角为θ,那么力F所做的功应当怎样计算？其中力F和位移s是向量，是F与s的夹角，而功是数量.|s||F|Wcos数量叫做力F与位移s的数量积cossF向量的夹角)1800(两个非零向量和，作，ab,OAaOBb�180与反向abOABabOAa0与同向abOABabaBbbAOBab则叫做向量和的夹角．记作ab90与垂直，abOABab注意:在两向量的夹角定义中,两向量必须是同起点的例1、如图，等边三角形中，求（1）AB与AC的夹角；（2）AB与BC的夹角。ABC通过平移变成共起点！12060'C平面向量的数量积的定义已知两个非零向量a和b，它们的夹角为，我们把数量叫做a与b的数量积（或内积），记作a·b，即cos||||bacos||||baba规定：零向量与任意向量的数量积为0，即0．0a（1）两向量的数量积是一个数量，而不是向量，符号由夹角决定（3）a·b不能写成a×b，a×b表示向量的另一种运算．（2）一种新的运算法则，以前所学的运算律、性质不适合．物理上力所做的功实际上是将力正交分解，只有在位移方向上的力做功．θsFbOBaOA，作，过点B作1BB垂直于直线OA，垂足为，则1B1OB|b|cosθOABab1BOABab)(1B|b|cosθ叫向量b在a方向上的投影．θ为锐角时，|b|cosθ＞0θ为钝角时，|b|cosθ＜0θ为直角时，|b|cosθ=0BOAab1B讨论总结性质：（1）e·a=a·e=|a|cos（2）a⊥ba·b=0(判断两向量垂直的依据)（3）当a与b同向时，a·b=|a|·|b|，当a与b反向时，a·b=-|a|·|b|．特别地aaaaaa||||2或（4）||||cosbaba（5）a·b≤|a|·|b|例1辨析题:1.若a≠0,且a·b=a·c,则b=c.2.(a·b)c=a(b·c).3.若a2-b2=0,则a=±b4.若|a·b|≥|a|·|b|，则ab.∥向量的数向量的数量积不满量积不满足结合律足结合律例题讲解例2．已知|a|=5，|b|=4，a与b的夹角，求a·b.120解：a·b=|a||b|cosθ120cos4510)21(45变式练习变式练习：若θ=120°呢？θ=90°呢？Δ.设|a|=12,|b|=9,a·b=-54√2求a和b的夹角.cos=a·b|a|·|b|=-54√212×9-√2∴=135°=2cos变式练习变式练习：若a·b=108√2呢？练习：1．若a=0，则对任一向量b，有a·b=0．2．若a≠0，则对任一非零向量b,有a·b≠0．3．若a≠0，a·b=0，则b=04．若a·b=0，则a·b中至少有一个为0．5．若a≠0，a·b=a·c，则b=c6．若a·b=a·c,则b≠c,当且仅当a=0时成立．7．对任意向量a有22||aa√×××××√5.6平面向量的数量积及运算律讨论总结性质：（1）e·a=a·e=|a|cos（2）a⊥ba·b=0(判断两向量垂直的依据)（3）当a与b同向时，a·b=|a|·|b|，当a与b反向时，a·b=—|a|·|b|．特别地aaaaaa||||2或（4）||||cosbaba（5）a·b≤|a|·|b|