高中数学 正弦定理和余弦定理课件 新人教A版必修5 课件VIP免费

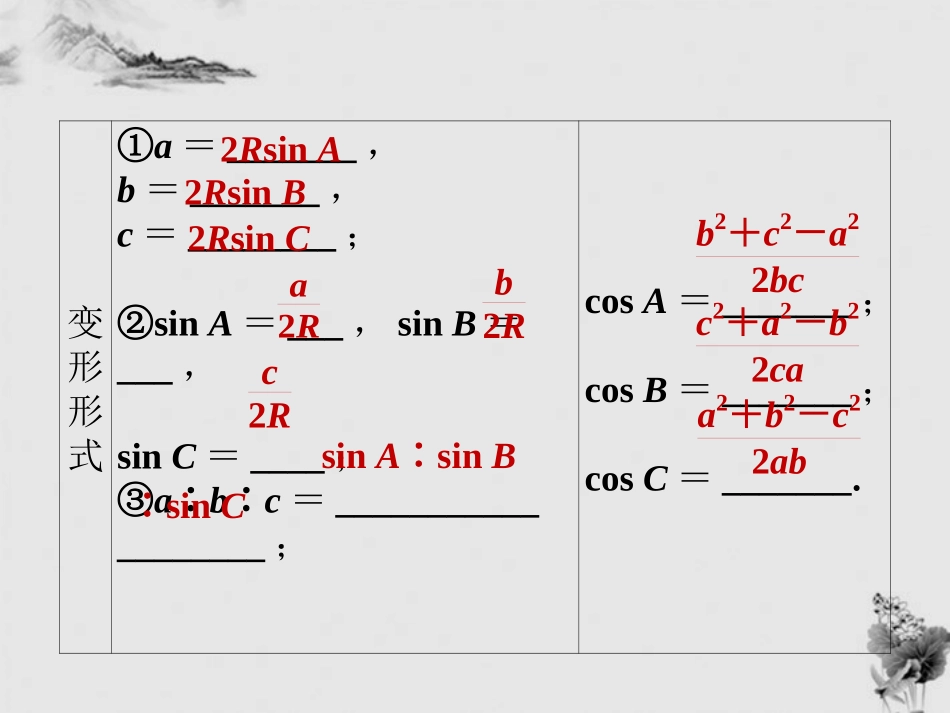
第7课时正弦定理和余弦定理正弦定理和余弦定理定理正弦定理余弦定理内容__________________＝2R(R为△ABC外接圆半径)a2＝________________，b2＝________________，c2＝____________________．b2＋c2－2bc·cosAc2＋a2－2ca·cosBa2＋b2－2ab·cosCasinA＝bsinB＝csinC变形形式①a＝_______，b＝_______，c＝________；②sinA＝___，sinB＝___，sinC＝____；③a∶b∶c＝___________________；cosA＝_______；cosB＝_______；cosC＝_______.2RsinA2RsinB2RsinCsinA∶sinB∶sinCa2Rb2Rc2Rb2＋c2－a22bcc2＋a2－b22caa2＋b2－c22ab变形形式④a＋b＋csinA＋sinB＋sinC＝asinA.【思考探究】在△ABC中，sinA＞sinB是A＞B的什么条件？提示：充要条件．因为sinA＞sinB⇔a2R＞b2R⇔a＞b⇔A＞B.1．已知△ABC，内角A、B、C的对边分别是a、b、c，a＝2，b＝3，B＝60°，则A等于()A．30°B．45°C．45°或135°D．30°或150°解析：由正弦定理得asinA＝bsinB，∴sinA＝asinBb＝2sin60°3＝22，又 2＜3，即a＜b，∴A＜B＝60°，∴A＝45°.答案：B2．△ABC的内角A、B、C的对边分别为a、b、c.若a、b、c成等比数列，且c＝2a，则cosB等于()A.14B.34C.24D.23解析：由已知得b2＝ac，c＝2a，∴cosB＝a2＋c2－b22ac＝5a2－2a24a2＝34.答案：B3．在△ABC中，若tanA＝34，C＝120°，BC＝23，则AB＝()A．3B．4C．5D．6解析：因为tanA＝34，所以sinA＝35，由正弦定理ABsinC＝BCsinA，可得AB＝BC·sinCsinA＝23×3235＝5.答案：C4．在△ABC中，如果A＝60°，c＝2，a＝6，则△ABC的形状是________．解析：由正弦定理asinA＝csinC，∴sinC＝12∴C＝30°(a>c，C只能是锐角)．答案：直角三角形5．在△ABC中，如果A＝60°，c＝4，a＝6，则三角形解的情况是________．解析： csinA＝4sin60°＝23＞6，∴三角形无解．答案：无解利用正、余弦定理解三角形1．利用正弦定理可解决以下两类三角形：一是已知两角和一角的对边，求其他边角；二是已知两边和一边的对角，求其他边角．2．利用余弦定理可解两类三角形：一是已知两边和它们的夹角，求其他边角；二是已知三边求其他边角．由于这两种情形下的三角形是唯一确定的，所以其解也是唯一的．(2010·浙江卷)在△ABC中，角A，B，C所对的边分别为a，b，c，已知cos2C＝－14.(1)求sinC的值；(2)当a＝2,2sinA＝sinC时，求b及c的长．解析：(1) cos2C＝1－2sin2C＝－14及0＜C＜π，所以sinC＝104.(2)当a＝2,2sinA＝sinC时，由正弦定理asinA＝csinC，得c＝4.由cos2C＝2cos2C－1＝－14及0＜C＜π，得cosC＝±64.由余弦定理c2＝a2＋b2－2abcosC，得b2±6b－12＝0(b＞0)，解得b＝6或26.所以b＝6，c＝4，或b＝26，c＝4.【变式训练】1.已知a、b、c分别是△ABC中角A、B、C的对边，且a2＋c2－b2＝ac.(1)求角B的大小；(2)若c＝3a，求tanA的值．解析：(1)由余弦定理，得cosB＝a2＋c2－b22ac＝12. 0＜B＜π，∴B＝π3.(2)方法一：将c＝3a代入a2＋c2－b2＝ac，得b＝7a.由余弦定理，得cosA＝b2＋c2－a22bc＝5714. 0＜A＜π，∴sinA＝1－cos2A＝2114.∴tanA＝sinAcosA＝35.方法二：将c＝3a代入a2＋c2－b2＝ac，得b＝7a.由正弦定理，得sinB＝7sinA. B＝π3，∴sinA＝2114.又b＝7a＞a，则B＞A，∴cosA＝1－sin2A＝5714.∴tanA＝sinAcosA＝35.方法三： c＝3a，由正弦定理，得sinC＝3sinA. B＝π3，∴C＝π－(A＋B)＝2π3－A.∴sin2π3－A＝3sinA.∴sin2π3cosA－cos2π3sinA＝3sinA.∴32cosA＋12sinA＝3sinA.∴5sinA＝3cosA.∴tanA＝sinAcosA＝35.利用正、余弦定理判断三角形形状依据已知条件中的边角关系判断三角形的形状时，主要有如下两种方法：(1)利用正、余弦定理把已知条件转化为边边关系，通过因式分解、配方等得出边的相应关系，从而判断三角形的形状；(2)利用正、余弦定理把已知条件转化为内角的三角函数间的关系，通过三角函数恒等变形，得出内角的关系，从而判断出三角形的形状，此时要注意应用A＋B＋C＝π这个结论．在△ABC中，a，b，c分别为内角A，B，C的对边，且2asinA＝(2b＋c)sinB＋(2c＋b)sinC.(1)求A的大小；(2)若sinB＋sinC＝1，试判断△ABC...