高中数学 12(命题及其关系、充分条件与必要条件)课件VIP免费

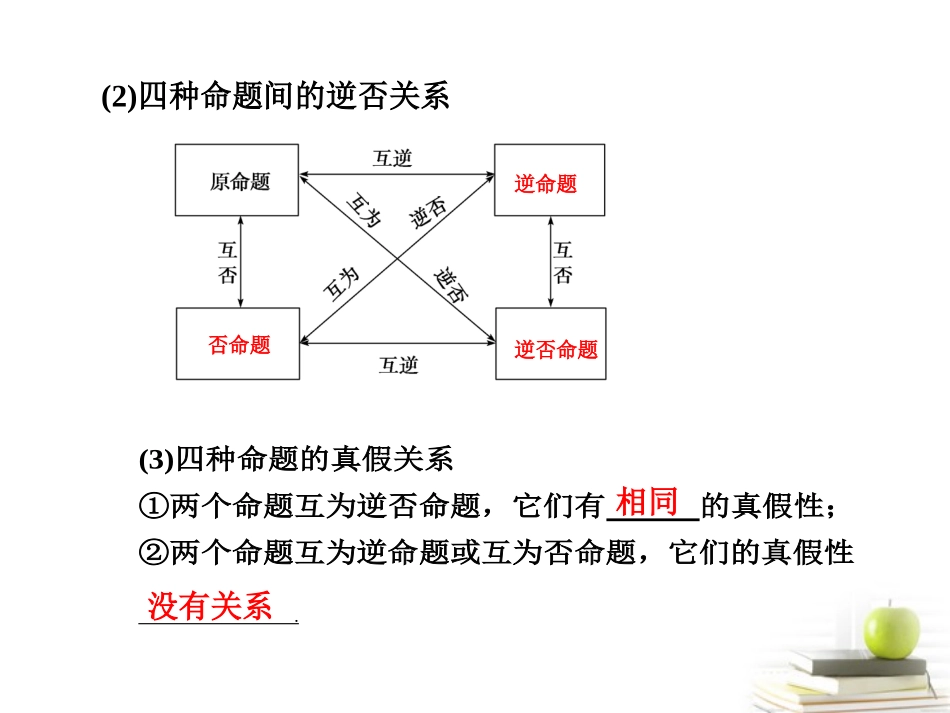
§1.2命题及其关系、充分条件与必要条件基础知识自主学习要点梳理1．命题的概念在数学中用语言、符号或式子表达的，可以的陈述句叫做命题．其中的语句叫真命题，的语句叫假命题．判断真假判断为真判断为假2．四种命题及其关系(1)四种命题命题表述形式原命题若p，则q逆命题否命题逆否命题若q，则p若綈p，则綈q若綈q，则綈p(2)四种命题间的逆否关系(3)四种命题的真假关系①两个命题互为逆否命题，它们有的真假性；②两个命题互为逆命题或互为否命题，它们的真假性.没有关系相同逆命题逆否命题否命题3．充分条件与必要条件(1)如果p⇒q，则p是q的，q是p的；(2)如果p⇒q，q⇒p，则p是q的.充分条件必要条件充要条件[难点正本疑点清源]1．用集合的观点，看充要条件设集合A＝{x|x满足条件p}，B＝{x|x满足条件q}，则有：(1)若A⊆B，则p是q的充分条件，若AB，则p是q的充分不必要条件；(2)若B⊆A，则p是q的必要条件，若BA，则p是q的必要不充分条件；(3)若A＝B，则p是q的充要条件；(4)若AB，且BA，则p是q的既不充分也不必要条件．2．从逆否命题，谈等价转换由于互为逆否命题的两个命题具有相同的真假性，因而，当判断原命题的真假比较困难时，可转化为判断它的逆否命题的真假．这就是常说的“正难则反”．基础自测1．下列命题中所有真命题的序号是________．①“a>b”是“a2>b2”的充分条件；②“|a|>|b|”是“a2>b2”的必要条件；③“a>b”是“a＋c>b＋c”的充要条件．解析①由2>－3⇒22>(－3)2知，该命题为假；②a2>b2⇒|a|2>|b|2⇒|a|>|b|，该命题为真；③a>b⇒a＋c>b＋c，又a＋c>b＋c⇒a>b；∴“a>b”是“a＋c>b＋c”的充要条件为真命题．②③2．下列命题：①“全等三角形的面积相等”的逆命题；②“若ab＝0，则a＝0”的否命题；③“正三角形的三个角均为60°”的逆否命题，其中真命题的序号是________(把所有真命题的序号填在横线上)．解析①“全等三角形的面积相等”的逆命题为“面积相等的三角形全等”，显然该命题为假命题；②“若ab＝0，则a＝0”的否命题为“若ab≠0，则a≠0”，而由ab≠0可得a，b都不为零，故a≠0，所以该命题是真命题；③由于原命题“正三角形的三个角均为60°”是一个真命题，故其逆否命题也是真命题．故填②③.②③3．已知a，b是实数，则“a>0且b>0”是“a＋b>0且ab>0”的____________条件．解析对于“a>0且b>0”可以推出“a＋b>0且ab>0”，反之也是成立的．充分必要4．(2010·福建)若向量a＝(x,3)(x∈R)，则“x＝4”是“|a|＝5”的()A．充分而不必要条件B．必要而不充分条件C．充要条件D．既不充分也不必要条件解析由x＝4知|a|＝42＋32＝5；反之，由|a|＝x2＋32＝5，得x＝4或x＝－4.故“x＝4”是“|a|＝5”的充分而不必要条件，故选A.A5．若集合A＝{1，m2}，B＝{2,4}，则“m＝2”是“A∩B＝{4}”的()A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件解析由“m＝2”可知A＝{1,4}，B＝{2,4}，所以可以推得A∩B＝{4}，反之，若“A∩B＝{4}”可以推得m2＝4，解得m＝2或－2，不能推得m＝2，所以“m＝2”是“A∩B＝{4}”的充分不必要条件．A题型分类深度剖析题型一四种命题及其关系例1设原命题是“当c>0时，若a>b，则ac>bc”，写出它的逆命题、否命题与逆否命题，并分别判断它们的真假．思维启迪先分清原命题的大前提，命题的条件和结论；再写其他命题．解“当c>0时”是大前提，写其他命题时应该保留，原命题的条件是a>b，结论是ac>bc.因此它的逆命题：当c>0时，若ac>bc，则a>b.它是真命题；否命题：当c>0时，若a≤b，则ac≤bc.它是真命题；逆否命题：当c>0时，若ac≤bc，则a≤b.它是真命题．探究提高在判断四个命题之间的关系时，首先要分清命题的条件与结论，再比较每个命题的条件与结论之间的关系，要注意四种命题关系的相对性，一旦一个命题定为原命题，也就相应的有了它的“逆命题”、“否命题”、“逆否命题”；要判定命题为假命题时只需举反例；对涉及数学概念的命题的判定要从概念本身入手．变式训练1若a、b、c∈R，写出命题“若ac<0，则ax2＋bx＋c＝0有两个不相等的实数根”的逆命题、否命题、逆否命题，并判断这三个命题的真...