高中数学一轮复习 平均变化率2课件 新人教A版 课件VIP免费

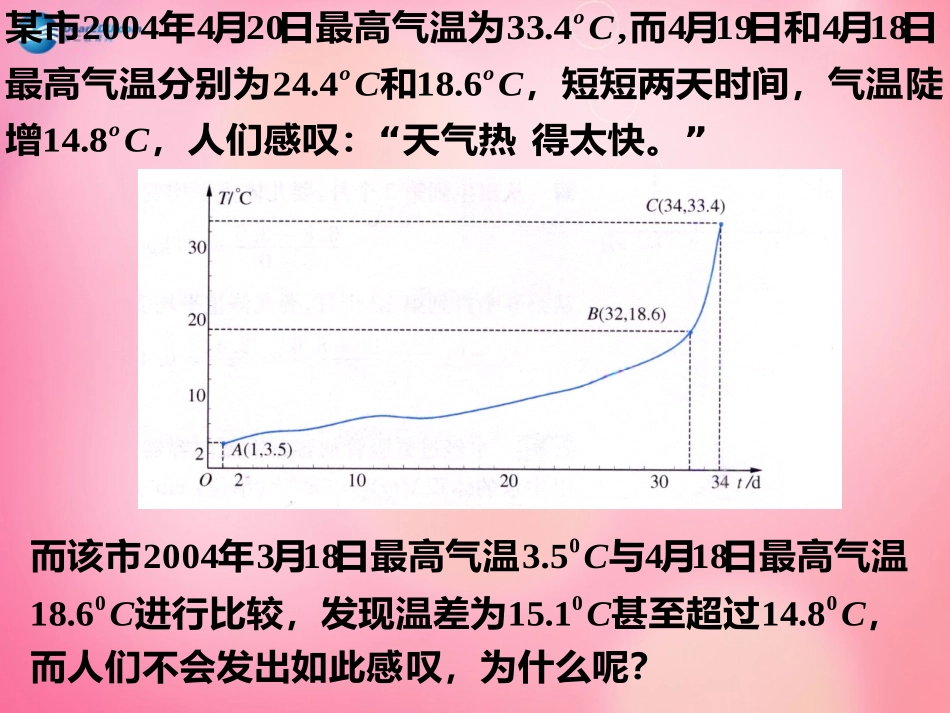
”得太快。“，人们感叹：天气热增陡，短短两天时间，气温和最高气温分别为日月日和月而日最高气温为月年某市CCCCoooo8.146.184.24184194,4.332042004叹，为什么呢？而人们不会发出如此感，甚至超过进行比较，发现温差为日最高气温月与日最高气温月年而该市CCCC00008.141.156.181845.318320042121121221)()()()(],[)(xxxfxfxxxfxfchangeofratesaveragexxxf）为（上的平均变化率在区间一般地，函数“”程度的数量化；平均变化率是曲线陡峭)1(注：但不能为零。可以为负，处的改变量可以为正也在表示自变量即为函数的增量；可令000),()()2(xxxxfxxfyxxfxxfxy)()(00。、求平均变化率、求xyy002;121、自阅例题率的意义。的侧重于理解平均变化、例例21上的平均变化率。，、，、，在区间求：已知函数例]9.01[]11[]21[)(,13)(3xfxxf上平均变化率。或为常数）在区间变式：求函数]),[](,[,(00002xxxxxxbabaxxy曲线上一点处的切线MNNM现在不动,沿着曲线运动,并且无限地向靠近,现在来观察运动的情况.,(),,,,N.CyfxCMNM如图设曲线是函数的图象在曲线上取一点及邻近的一点过两点作割线一、切线问题。附近越来越逼近曲线在点运动，割线向点沿曲线随着点LPMNMLN处的切线。也称为曲线在点直线，这条处最逼近曲线就成为在点最终时，直线无限逼近当点MTTMMNMN:(),,,CyfxMNNMMNMTMTM曲线上有两点当点沿着曲线无限接近于点如果割线有一个极限位置那么直线叫做曲线在点处的切线.CMxyo0xT1xN0y1y切线的定义在点求曲线L：)(xfy),(00yxM处切线的斜率。割线MN的极限位置MT称为曲线L在点M处的切线。割线MN的斜率为：tanxxfxxf)()(000x当时,xyLMxyo0xT1xN0yx切线斜率1yy切线MT的斜率为：xxfxxf)()(00tank0无限趋近于x例题讲解。，)2,1(，1(1)：2以及切线的方程处的切线的斜率那么求此曲线在点曲线的方程为例Pxy。)38,2(31)2(3处的切线方程在点求曲线Pxy