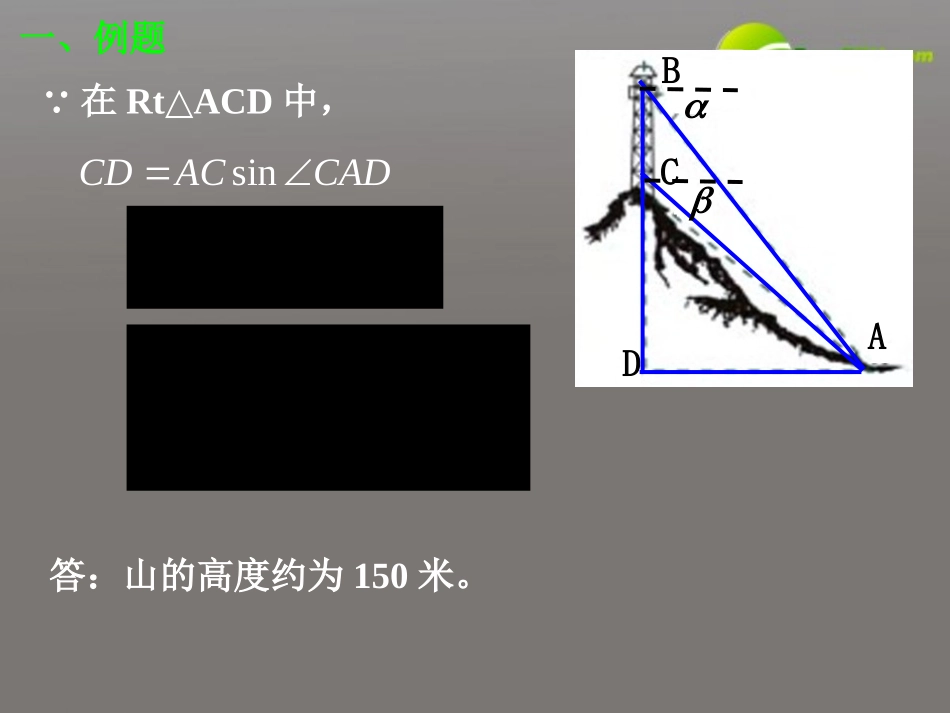
例1.在山顶铁塔上B处测得地面上一点A的俯角=54°40′,在塔底C处测得A处的俯角=50°1′。已知铁塔BC部分的高为27.3m,求出山高CD(精确到1m)解:依题意可知,在△ABC中,∠ABC=90o-,∠BAD=,∠CAD=∴∠BAC=-∵根据正弦定理,sinsinBCACBACABCsinsin(90)cossinsin()sin()BCABCBCBCACBAC一、例题ABCD''''sincossinsin()27.3cos5440sin501sin(5440501)150()CDACCADBCm答:山的高度约为150米。∵在RtACD△中,ABCD一、例题例2.如图,AB是底部B不可到达的一个建筑物,A为建筑的最高点,试设计一种测量建筑物高度AB的方法。解:选择一条水平基线HG,使H、G、B三点在同一条直线上。在H、G两点用测角仪器测得A的仰角分别是、,CD=a,测角仪器的高是h,那么,在△ACD中,根据正弦定理可得sinsinsinsin()CDADCaACCADABAEh一、例题sinAChsinsinsin()ah例3.一辆汽车在一条水平的公路上向正西行驶,到A处时测得公路南侧远处一山顶D在西偏北15o的方向上,行驶5km后到达B处,测得此山顶在西偏北30o的方向上,仰角15o,求此山的高度CD.一、例题ADCB30o15o15o一、例题例4.AQCPBa二、练习P15第1题ABCD二、练习P15第2题ABCD30o45o200m二、练习30o45oh第3题三、作业