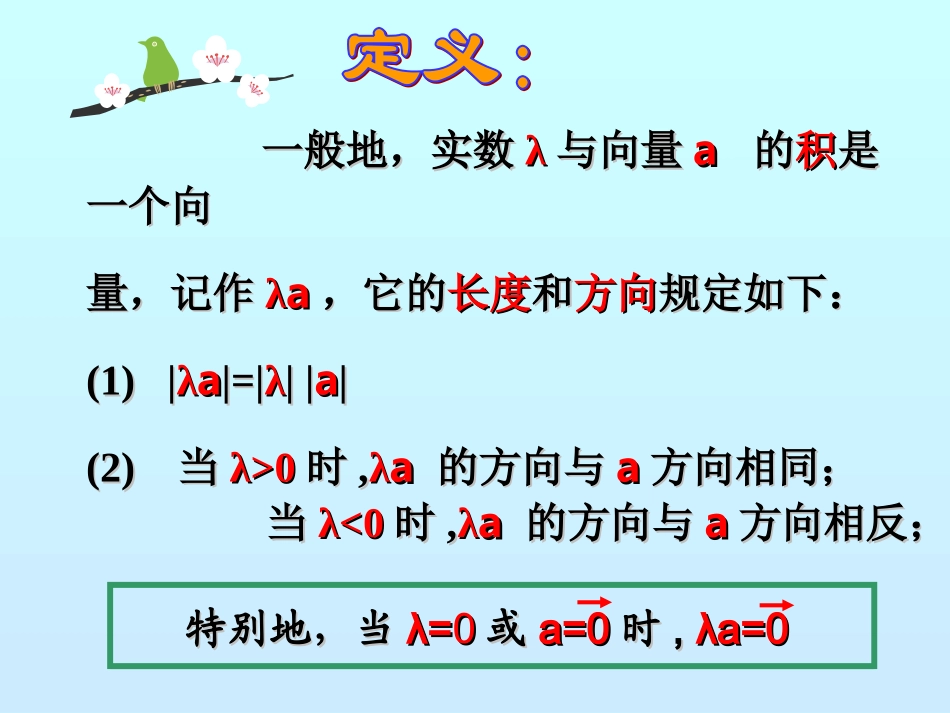
2.4.1平面向量数量积的物理背景及其含义一般地,实数一般地,实数λλ与向量与向量aa的的积积是是一个一个向向量量,记作,记作λλaa,它的,它的长度长度和和方向方向规定如下:规定如下:(1)|(1)|λλaa|=||=|λλ||||aa||(2)(2)当当λ>0λ>0时时,,λλaa的方向与的方向与aa方向相同;方向相同;当当λ<0λ<0时时,,λλaa的方向与的方向与aa方向相反;方向相反;特别地,当特别地,当λ=λ=00或或a=0a=0时时,,λa=0λa=0设设a,ba,b为任意向量,为任意向量,λ,μλ,μ为为任意实数任意实数,则有:,则有:①①λλ((μμaa)=()=(λμλμ))aa②②((λ+μλ+μ))a=a=λλa+a+μμaa③③λλ((a+ba+b)=)=λλa+a+λλbb已知两个非零向量a和b,作OA=a,OB=b,则∠AOB=θ(0°≤θ≤180°)叫做向量a与b的夹角。OBAθ当θ=0°时,a与b同向;OAB当θ=180°时,a与b反向;OABB当θ=90°时,称a与b垂直,记为a⊥b.OAab我们学过功的概念,即一个物体在力F的作用下产生位移s(如图)θFS力F所做的功W可用下式计算W=|F||S|cosθ其中θ是F与S的夹角从力所做的功出发,我们引入向量“数量积”的概念。已知两个非零向量a与b,它们的夹角为θ,我们把数量|a||b|cosθ叫做a与b的数量积(或内积),记作a·ba·b=|a||b|cosθ规定:零向量与任一向量的数量积为0。|a|cosθ(|b|cosθ)叫做向量a在b方向上(向量b在a方向上)的投影。注意:向量的数量积是一个数量。向量的数量积是一个数量,那么它什么时候为正,什么时候为负?a·b=|a||b|cosθ当0°≤θ<90°时a·b为正;当90°<θ≤180°时a·b为负。当θ=90°时a·b为零。设ba、是非零向量,be是与方向相同的单位向量,ea与是的夹角,则cos||)1(aeaae0)2(baba|;|||)3(bababa同向时,与当|;|||bababa反向时,与当特别地2||aaaaaa||或2a||||cos)4(baba||||||)5(babaOABθabB1||||cosabab例1已知|a|=5,|b|=4,a与b的夹角θ=120°,求a·b。OABθ|b|cosθabB1ba等于a的长度||a方向上的投影在ab与cos||b的乘积。练习:1.若a=0,则对任一向量b,有a·b=0.2.若a≠0,则对任一非零向量b,有a·b≠0.3.若a≠0,a·b=0,则b=04.若a·b=0,则a·b中至少有一个为0.5.若a≠0,a·b=b·c,则a=c6.对任意向量a有22||aa√××××√二、平面向量的数量积的运算律:数量积的运算律:cbcacbabababaabba))(3()()())(2()1(其中,cba、、是任意三个向量,R则(a+b)·c=ON|c|=(OM+MN)|c|=OM|c|+MN|c|=a·c+b·c.ONMa+bbac向量a、b、a+b在c上的射影的数量分别是OM、MN、ON,证明运算律(3)注:?)()(cbacba例3:求证:(1)(a+b)2=a2+2a·b+b2;(2)(a+b)·(a-b)=a2-b2.证明:(1)(a+b)2=(a+b)·(a+b)=(a+b)·a+(a+b)·b=a·a+b·a+a·b+b·b=a2+2a·b+b2.例3:求证:(1)(a+b)2=a2+2a·b+b2;(2)(a+b)·(a-b)=a2-b2.证明:(2)(a+b)·(a-b)=(a+b)·a-(a+b)·b=a·a+b·a-a·b-b·b=a2-b2.5.||3,||4,abkakbakb例已知当且仅当为何值时,向量与互相垂直?例42)(3)abab求(。||6,||4,abab已知与60,o的夹角为作业:)(,2432,1||||1cbacabacbakbakbababa求证:是非零向量,且、设的值。互相垂直,求也与且、若3、用向量方法证明:直径所对的圆周角为直角。ABCO如图所示,已知⊙如图所示,已知⊙OO,,ABAB为直径,为直径,CC为⊙为⊙OO上任意一点。求证∠上任意一点。求证∠ACB=90°ACB=90°分析:要证∠ACB=90°,只须证向量,即。ACCB�0ACCB�解:解:设则,由此可得:,AOaOCb�,ACabCBab�ACCBabab�2222||||abab220rr即,∠ACB=90°0CBAC