高三数学(导数)全章课件：1导数的概念 课件VIP免费

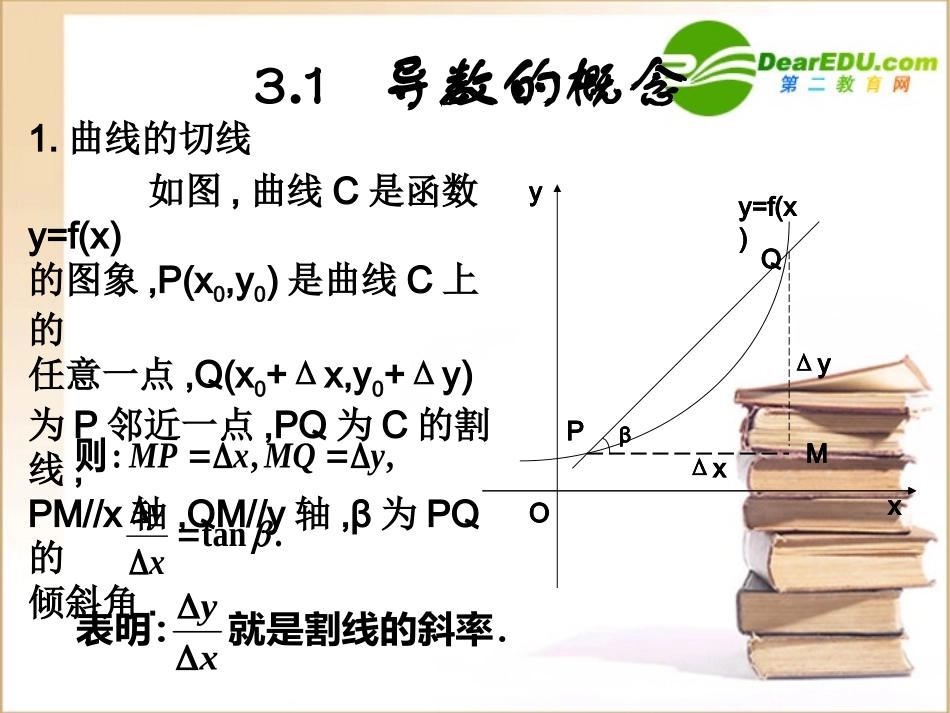
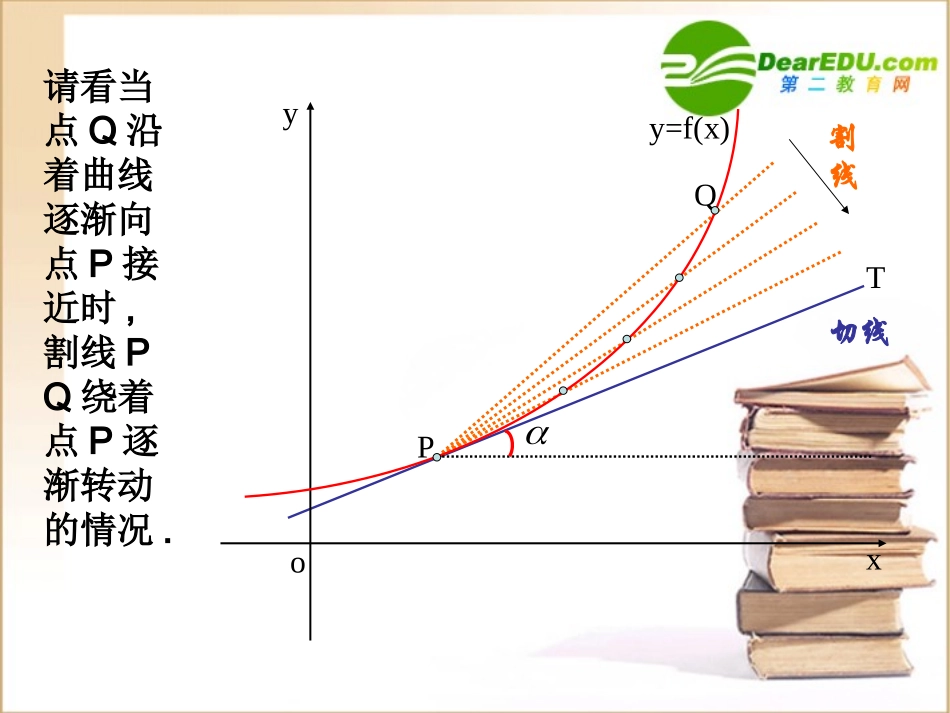
导数的概念3.1导数的概念1.曲线的切线βy=f(x)PQMΔxΔyOxyβPy=f(x)QMΔxΔyOxy如图,曲线C是函数y=f(x)的图象,P(x0,y0)是曲线C上的任意一点,Q(x0+Δx,y0+Δy)为P邻近一点,PQ为C的割线,PM//x轴,QM//y轴,β为PQ的倾斜角..tan,,:xyyMQxMP则.就是割线的斜率表明：xyPQoxyy=f(x)割线切线T请看当点Q沿着曲线逐渐向点P接近时,割线PQ绕着点P逐渐转动的情况.我们发现,当点Q沿着曲线无限接近点P即Δx→0时,割线PQ有一个极限位置PT.则我们把直线PT称为曲线在点P处的切线.设切线的倾斜角为α,那么当Δx→0时,割线PQ的斜率,称为曲线在点P处的切线的斜率.即:xxfxxfxykxx)()(limlimtan0000切线这个概念:①提供了求曲线上某点切线的斜率的一种方法;②切线斜率的本质——函数平均变化率的极限.要注意,曲线在某点处的切线:1)与该点的位置有关;2)要根据割线是否有极限位置来判断与求解.如有极限,则在此点有切线,且切线是唯一的;如不存在,则在此点处无切线;3)曲线的切线,并不一定与曲线只有一个交点,可以有多个,甚至可以无穷多个.例1:求曲线y=f(x)=x2+1在点P(1,2)处的切线方程.QPy=x2+1xy-111OMyx.2)(2lim)11(1)1(lim)()(lim:2020000xxxxxxxfxxfkxxx解因此,切线方程为y-2=2(x-1),即y=2x.求曲线在某点处的切线方程的基本步骤:先利用切线斜率的定义求出切线的斜率,然后利用点斜式求切线方程.例2:已知曲线上一点P(1,2),用斜率的定义求过点P的切线的倾斜角和切线方程.222xy,22)1(2)1()1(,lim:20xfxfyxyKxP而解.12212422)1(24lim]22)1(2[)(24lim22)1(2limlim20220200xxxxxxxxxyxxxx.45,45,1tan等于点切线的倾斜角即过PKP故过点P的切线方程为:y-2=1•(x-1),即y=x+1.练习:求曲线上一点P(1,-1)处的切线方程.31xy答案:y=3x-4.2.瞬时速度已知物体作变速直线运动,其运动方程为s＝s(t)(ｓ表示位移,t表示时间),求物体在t0时刻的速度．OA0A1sss(t)s=如图设该物体在时刻t0的位置是ｓ(t0)＝OA0,在时刻t0+Δt的位置是s(t0+Δt)=OA1,则从t0到t0+Δt这段时间内,物体的位移是:在时间段(t0+t)－t0=t内，物体的平均速度为:tsttttsttsv0000__)()()()()(0001tsttsOAOAs平均速度反映了物体运动时的快慢程度,但要精确地描述非匀速直线运动,就要知道物体在每一时刻运动的快慢程度,也即需要通过瞬时速度来反映.如果物体的运动规律是s=s(t)，那么物体在时刻t的瞬时速度v，就是物体在t到t+Δt这段时间内，当Δt0时的平均速度:.)()(limlim00ttsttstsvtt例1:物体作自由落体运动,运动方程为：其中位移单位是m,时间单位是s,g=10m/s2.求：(1)物体在时间区间[2,2.1]上的平均速度；(2)物体在时间区间[2,2.01]上的平均速度；(3)物体在t=2(s)时的瞬时速度.221gts解:)(212__tggtsvsss(2+t)Os(2)(1)将Δt=0.1代入上式，得:./5.2005.2__smgv(2)将Δt=0.01代入上式，得:./05.20005.2__smgv的极限为：从而平均速度当__,22,0)3(vtt./202limlim0__0smgtsvvtt即物体在时刻t0=2(s)的瞬时速度等于20(m/s).当时间间隔Δt逐渐变小时,平均速度就越接近t0=2(s)时的瞬时速度v=20(m/s).练习:某质点沿直线运动,运动规律是s=5t2+6,求:(1)2≤t≤2+Δt这段时间内的平均速度,这里Δt取值范围为1;(2)t=2时刻的瞬时速度..520,)(520)625(6)2(5)1(:222ttsttts故平均速度为：解.25,1tst时当.20)520(limlim:2)2(00ttsttt时刻的瞬时速度为3.导数的概念从上面两个实例,一个是曲线的切线的斜率,一个是瞬时速度,具体意义不同,但通过比较可以看出它们的数学表达式结构是一样的,即计算极限,这就是我们要学习的导数的定义.xyx0lim定义：设函数y=f(x)在点x0处及其附近有定义,当自变量x在点x0处有改变量Δx时函数有相应...