高一数学平面向量的数量积 苏教版 课件VIP免费

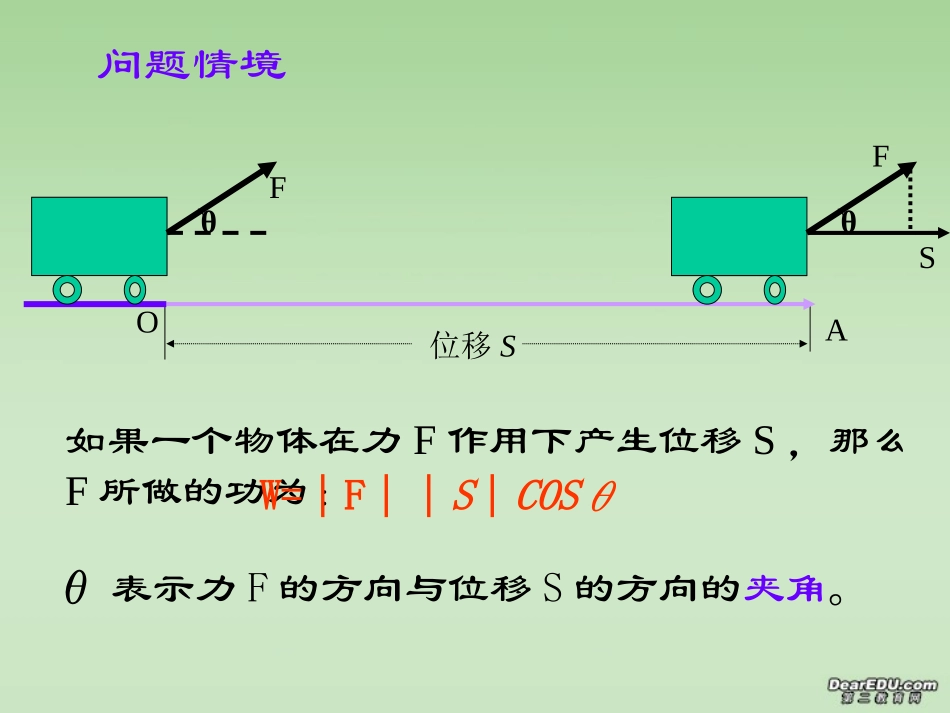
平面向量的数量积如果一个物体在力F作用下产生位移S，那么F所做的功为:θ表示力F的方向与位移S的方向的夹角。位移SOA问题情境θFFθSW=│F││S│COSθ看课本78-79页并思考如下问题：1、向量的夹角是如何定义（规定）的？2、向量的数量积如何定义，它与物理中力做功有什么联系？3、向量的数量积是向量吗？向量在方向上的投影是向量吗？4、平面向量的数量积有什么样的几何意义？1、向量的夹角已知两个非零向量a和b，在平上任取一点O，作OA=a,OB=b,则叫做向量a与b的夹角(1)中OA与OB的夹角为（2）中OA与OB的夹角为（3）中OA与OB的夹角为AOB（当时，a与b＿＿；当时，a与b＿＿；当时，a与b＿＿，记作）018090（4）中OA与OB的夹角为反向同向ba垂直指出下列图中两向量的夹角AOABBBB.AAOOO.(2)(4)(3)(1))1800(AOB18002、数量积的定义已知两个非零向量a和b，它们的夹角为，我们把数量叫做向量a与b的数量积（或内积）记作即并规定cosbabacosbaba00a思考1：在平面向量的数量积定义中，它与两个向量的加减法有什么本质区别？向量的加减的结果还是向量，但向量的数量积结果是一个数量（实数）。（这个数量的大小与两个向量的长度及其夹角有关）│b│COSθ叫做向量b在向量a上的投影。1B)(1B1B(1)思考2：在下列各图中作出│b│COSθ的几何图形，并说明它的几何意义是什么？OAB(2)abOAB(3)ababAO过b的终点B作OA＝a的垂线段，垂足为，则由直角三角形的性质得=│b│COSθ1BB1B1OB投影是向量吗投影是一个数值（实数），当θ为锐角时，它是正值；当θ为钝角时，它是负值。时│b│COSθ＝＿＿时│b│COSθ＝＿＿时│b│COSθ＝＿＿018090－│b││b│0数量积ab•等于a的长度│a│与b在a的方向上的投影│b│COSθ的积ab•的几何意义：3、向量数量积的几何意义ab=•│a││b│COSθabθOBOB＝│b│COSθ4、向量数量积的性质设a,b都是非零向量，e是与b的方向相同的单位向量，θ是a与e的夹角，则(1)e•a=__________;a•e=_________(2)ab____a•b=0(3)当a与b同向时，a•b=________当a与b异向时，a•b=___________a•a=________(4)│a•b│___│a││b│(5)cos＝______│a│COSθ│a│COSθ│a││b│-│a││b│2ababaab=•│a││b│COSθe•a=a•e=│a│COSθ性质4向量数量积的运算律•1．a·b=b·a•2.(λ·a)b=a·(λb)=λ(a·b)=λa·b•3.(a+b)·c=a·c+b·c根据定义不难验证运算律1,2的正确性,运算律3的证明参见链接.ab=•│a││b│COSθ（1）若a=0，则对任意向量b，有ab=•0（）（2）若a0，则对任意非零向量b，有ab•0()（3）若a0，且ab•=0，则b=0（）（4）若ab•=0，则a=0或b=0（）（5）对任意向量a有（）（6）若a0，且ab=ac••，则b=c（）5、反馈练习:判断正误a=|a|²²××××√√向量的数量积是向量之间的一种乘法，与数的乘法是有区别的,1:平行且方向相同与因为解BCAD.0的夹角为与BCAD91330cosBCADBCAD6、典型例题分析92ADBCAD或BCAD.1:,60DAB3,AD4,ABABCD,图求中，在平行四边形如CDAB.2ab=•│a││b│COSθBACD60DAAB)3(且方向相反平行与,.2CDAB180的夹角是与CDAB16144180cosCDABCDAB162ABCDAB或,60.3的夹角是与ADAB120的夹角是与DAAB62134120cosDAABDAAB例题CDAB.2DAAB.3BACD60120进行向量数量积计算时,既要考虑向量的模,又要根据两个向量方向确定其夹角ab=•│a││b│COSθ24钝角直角230－20254ab=•│a││b│COSθ7、课时作业：1、已知|p|＝8，|q|＝6，p和q的夹角是60°，求p•q2、设|a|＝12，|b|＝9，a•b＝－，求a和b的夹角3、已知中，AB＝a，AC＝b当a•b<0时，是＿＿＿三角形；当a•b=0时，是＿＿＿三角形4、已知|a|＝6，e为单位向量，当它们的夹角分别为45°、90°、135°时，求出a在e方向上的投影5、已知中a＝5，b＝8，∠C＝60°，求BCCA•ABCABCABCABC作业5231358...