高中数学 231向量数乘运算课件 北师大版必修4 课件VIP免费

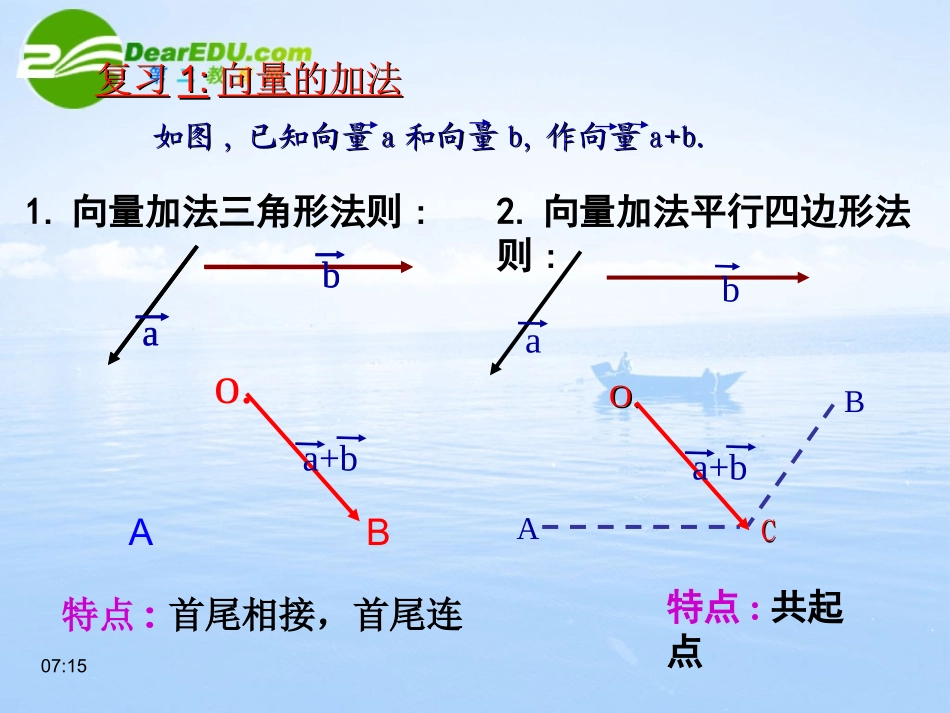
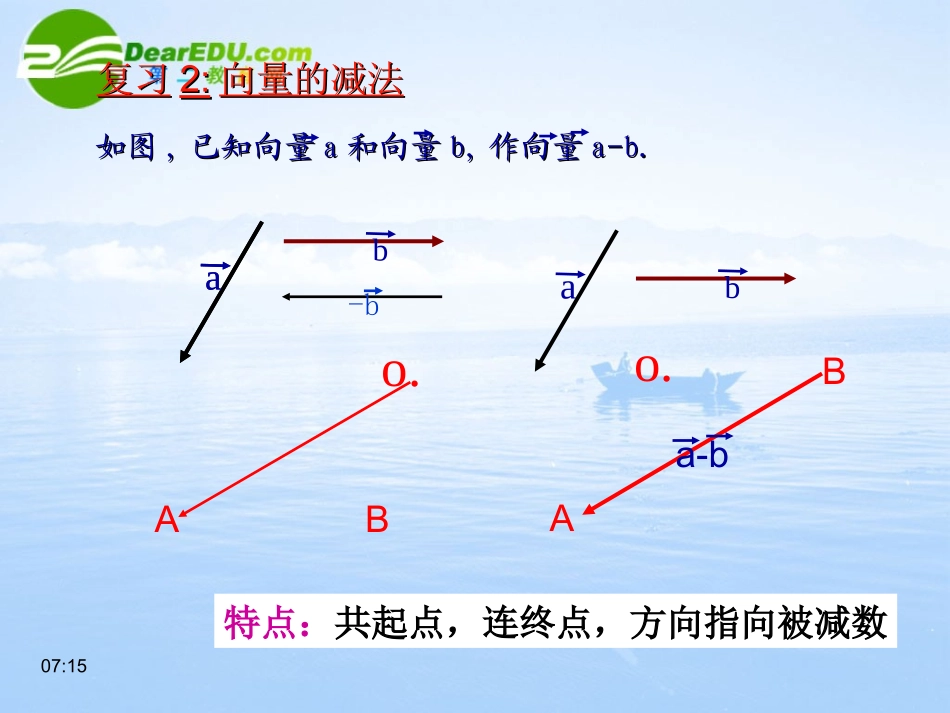
2.3.1从速度倍数到数乘向量07:15复习复习1:1:向量的加法向量的加法BA如图如图,,已知向量已知向量aa和向量和向量b,b,作向量作向量a+b.a+b.bao.OO..CCa+bbaABba+ba1.向量加法三角形法则:2.向量加法平行四边形法则:特点:首尾相接，首尾连特点:共起点07:15复习复习2:2:向量的减法向量的减法o.BAa-b如图如图,,已知向量已知向量aa和向量和向量b,b,作向量作向量a-b.a-b.aba-bo.BAab特点：共起点，连终点，方向指向被减数实际背景表示，试画出该向量。用秒的位移对应的向量那么在同方向上向量，一秒钟的位移对应一物体作匀速直线运动aa33,aa3在物理中位移与速度的关系：s=vt，力与加速度的关系：f=ma.其中位移、速度，力、加速度都是向量，而时间、质量都是数量讲授新课思考题1:已知向量如何作出和a,aaa(a)(a)(a)?aOAaBaCaNMQPaaaOCOAABBCaaa�记:aaa3a即:OC3a.�同理可得:PN(a)(a)(a)3a�思考题2:向量与向量有什么关系?向量与向量有什么关系?3aaa3a(1)向量的方向与的方向相同,向量的长度是的3倍,即3aaa3a3a3a.(2)向量的方向与的方向相反,向量的长度是的3倍,即3aa3aa3a3a.07:1507:15定义定义::特别地，当特别地，当λ=0λ=0或或a=0a=0时时,λa=0,λa=0(2)(2)方向当方向当λ>0λ>0时时,λa,λa的方向与的方向与aa方向相同；方向相同；当当λ<0λ<0时时,λa,λa的方向与的方向与aa方向相反；方向相反；(1)(1)长度长度|λa|=|λ||λa|=|λ|··|a||a|一般地一般地，实数，实数λλ与向量与向量aa的积是一个向量，这种的积是一个向量，这种运算叫做运算叫做向量的数乘运算向量的数乘运算，记作，记作λaλa。。它的长度和方向规定如下它的长度和方向规定如下：：07:15练习练习2:2:结论:2a+2b2b(2)已知向量a,b，求作向量2(a+b)和2a+2b，并比较。ab结论:2a+2b=2(a+b)a+b6a3(2a)a2(a+b)2a3(2a)=6a(2+4)a=2a+4a(1)根据定义，求作向量3(2a)和(6a)(a≠0)，并比较。①①λ(μa)=(λμ)aλ(μa)=(λμ)a运算律:设a、b为任意向量，λ、μ为任意实数，则有：②②(λ+μ)a=λa+μa(λ+μ)a=λa+μa③③λ(a+b)=λa+λbλ(a+b)=λa+λb2(a+b)数乘向量的运算律：aa结合律aaa第一分配律baba第二分配律07:15练习3:解:(1)原式=(2)原式=(3)原式=计算：(口答)(1)(-3)×4a(2)3(a+b)–2(a-b)-a(3)(2a+3b-c)–(3a-2b+c)(3-2-1)a+(3+2)b=5b(2-3)a+(3+2)b+(-1-1)c=-a+5b-2c-12a向量的加、减、数乘运算统称为向量的线形运算。对于任意的向量a,b以及任意实数λ,μ,恒有λ(μ1a±μ2b)=λμ1a±λμ2b07:15思考:判定定理:当a与b同方向时，有b=μa;当a与b反方向时，有b=-μa，所以始终有一个实数λ，使b=λa。1、如果b=λa,那么，向量a与b是否共线？2、如果非零向量a与b共线，那么是否有λ，使b=λa？对于向量a(a≠0)、b，如果有一个实数λ，使得b=λa,那么，由数乘向量的定义知：向量a与b共线。若向量a与b共线，a≠0，且向量b的长度是a的长度的μ倍，即有|b|=μ|a|,且aa是一个非零向量，若存在一个实数是一个非零向量，若存在一个实数λλ，，使得使得b=b=λλaa，则向量，则向量bb与非零向量与非零向量aa共线共线2)2)bb可以是零向量吗可以是零向量吗??思考思考:1):1)aa为什么要是非零向量为什么要是非零向量??向量b与非零向量a共线当且仅当有唯一一个实数λ，使得b=λa.07:15例题1:AEDCB解：=3AC=3(AB+BC)∵AB+BC=AC=3AB+3BC又AE=AD+DE∴AC与AE共线如图，已知AD=3AB、DE=3BC，试判断AC与AE是否共线?变：若B、C分别是AD、AE的三等分点，证明：BC‖DE。07:15例题2:解：作图如右OABC依图猜想:A、B、C三点共线∴A、B、C三点共线.abbb已知任意两非零向量a、b，试作OA=a+b,OB=a+2b,OC=a+3b。你能判断A、B、C三点之间的位置关系吗？为什么？ba∵AB=OB-OA∴AC=2AB又AC=OC-OA=a+3b-(a+b)=2b=a+2b-(a+b)=b又AB与AC有公共点A，APBCa例3ABC平面内的三点，切A与B不重合，P是平面内任意一点，若点C在AB上，则存在实数λ，使得PC=λPA+(1-λ)PB07:15小结回顾:二、知识应用：1.证明向量共线；2.证明三点共线:AB=λBCA,B,CAB=λBCA,B,C三点共线；三点共线；3.证明两直线平行:AB=λCDAB∥CDAB=λCDAB∥CDABAB、、CDCD不重合不重合直线AB∥直线CD一、概念与定理①λa的定义及运算律②向量共线定理(a≠0)b=λa向量a与b共线07:15作业作业::创新作业创新作业谢谢谢谢!!