高中数学 124( 诱导公式)课件(2) 新人教B版必修4 课件VIP免费

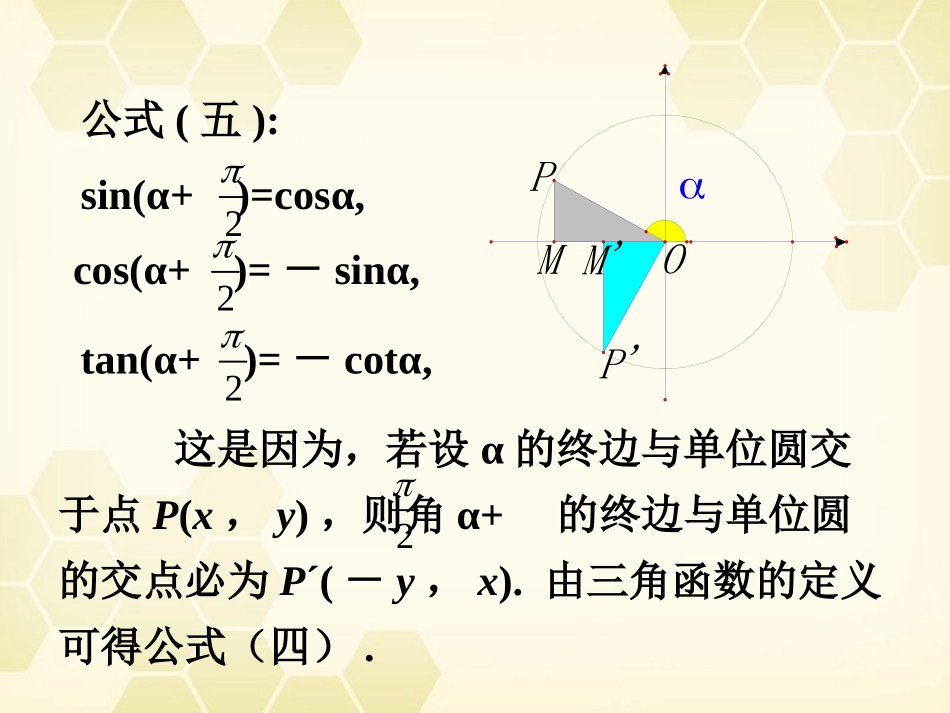
1.2.4诱导公式（二）公式(五):sin(α+)=cosα,2cos(α+)=－sinα,2tan(α+)=－cotα,2P'OPMM'这是因为，若设α的终边与单位圆交于点P(x，y)，则角α+的终边与单位圆的交点必为P´(－y，x).由三角函数的定义可得公式（四）.2公式(六):sin(－α+)=cosα,2cos(－α+)=sinα,2tan(－α+)=cotα,2-P'(x,y)P(x,y)yxO四组诱导公式的作用:任意一个角都可以表示为的形式。)4(2其中k这样由前面的公式就可以把任意角的三角函数求值问题转化为0到之间角的三角函数求值问题。4这样，诱导公式可以分为两大组：(1)由2kπ+α，－α，π+α，π－α等为一组，所得到的三角函数与原来的三角函数是相同三角函数；(2)由+α，－α为一组，所得到的三角函数与原来的三角函数是互余的三角函数；22记忆口诀：奇变偶不变.所有的诱导公式的符号是由角度所在象限决定的，即把角α看做锐角，原来角度所在象限，原来函数所具有的符号为公式右边的符号。记忆口诀：符号看象限.例1求证：)2cos()5cos()2sin()4sin()cot()2tan()23cos()2sin(kkk证：cossintancot左边sincoscossinsincoscossin右边sincoscossin左边=右边.∴原等式成立.例2.22cos[()]cos()244原式的值。求)4(cos)4(cos22解：22sin()cos()44=1.例3.已知sinβ=，sin(α+β)=1，求sin(2α+β).31解：)(221)sin(Zkk从而sin(2)sin[2(2)]2ksin(4)k=sin(π－β)=sinβ=31例4.已知f(cosx)=cos17x，求f(sinx)解：f(sinx)=f[cos(90◦－x)]=cos[17×(90◦－x)]=cos(4×360◦+90◦－17x)=cos(90◦－17x)=sin17x.课堂练习：1．计算：sin315sin(480)+cos(330).解：原式=sin(36045)+sin(360+120)+cos(360+30)=sin45+sin60+cos302322．已知的值。，求)65cos(33)6cos(解：55cos()cos[()]66cos()6333．求证：Zkkkkk,1])1cos[(])1sin[()cos()cos(证：若k是偶数，即k=2n(nZ)则：cos(2)cos(2)sin[2()]cos[2()]nnnn左边sincossin(cos)=－1若k是奇数，即k=2n+1(nZ)则：cos[2()]cos[2()]sin[2(1))]cos[2(1))]nnnn左边sin(cos)sincos=－1∴原式成立.5．已知：2tan(),|cos()|cos,a1cos()求的值。解：由题设：2tan0,|cos|cos,acos0即由此：当a0时，tan<0,cos<0,为第二象限角，421tan1seccos1a原式当a=0时，tan=0,=k,cos∴=±1，∵cos≤0，∴cos=1,)0(11cos14aa原式综上所述：411cos()a6．若关于x的方程2cos2(+x)sinx+a=0有实根，求实数a的取值范围。解：原方程变形为：2cos2xsinx+a=0，即22sin2xsinx+a=0∴817)41(sin22sinsin222xxxa∵1≤sinx≤1∴81741sinminax时，当817)41(sin22sinsin222xxxa11sinmaxax时，当∴a的取值范围是[].1,817小结:应用诱导公式化简三角函数的一般步骤：1用“”公式化为正角的三角函数；2用“2k+”公式化为[0，2]角的三角函数；3用“±”或“2”公式化为锐角的三角函数.