高中数学 (直接证明与间接证明)课件16 新人教A版选修1-2 课件VIP免费

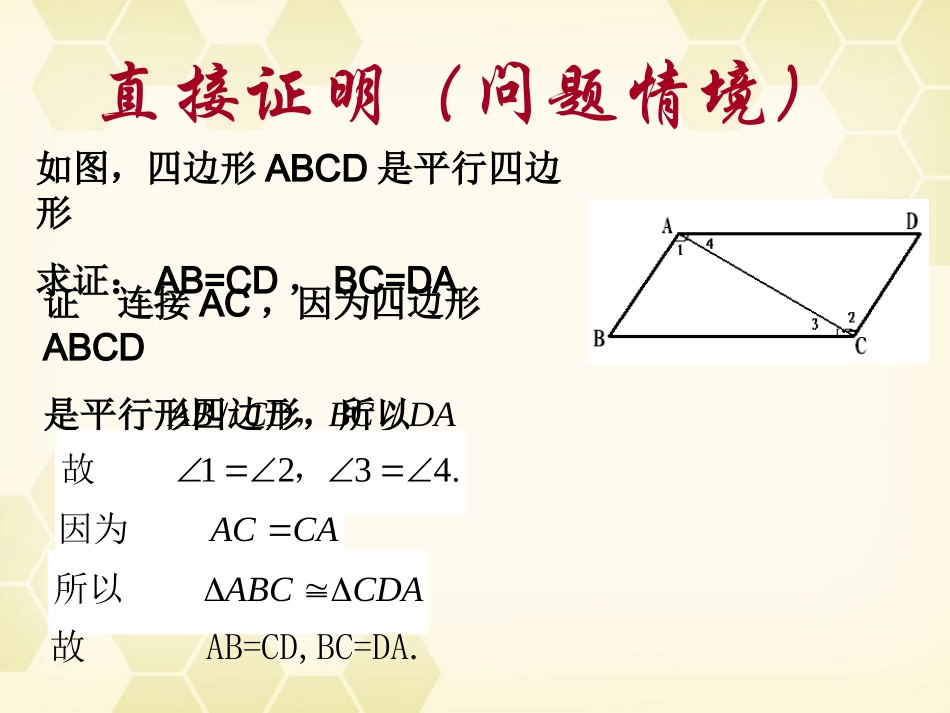
2.2直接证明(一)直接证明（问题情境）如图，四边形ABCD是平行四边形求证：AB=CD，BC=DA证连接AC，因为四边形ABCD是平行形四边形，所以DABCCDAB////，.4321，故CAAC因为CDAABC所以故AB=CD,BC=DA.直接证明1概念直接从原命题的条件逐步推得命题成立2直接证明的一般形式：本题结论已知定理已知公理已知定义本题条件直接证明（学生活动）?)0,0(25babaab基本不等式何证明（必修）》中，我们如思考：在《数学证法1对于正数a,b,有abbaabbaabbaba220202）（直接证明证法2要证只要证只要证只要证2baabbaab2baba202)(0ba因为最后一个不等式成立，故结论成立。直接证明（数学理论）上述两种证法有什么异同？都是直接证明证法1从已知条件出发，以已知的定义、公理、定理为依据，逐步下推，直到推出要证明的结论为止综合法相同不同证法2从问题的结论出发，追溯导致结论成立的条件，逐步上溯，直到使结论成立的条件和已知条件吻合为止分析法直接证明综合法和分析法的推证过程如下：综合法已知条件结论分析法结论已知条件直接证明（例题）.1DFCEBFAEBDOACOOCDAB，求证：，，交于点，如图，已知例直接证明证（综合法）因为BDOACO因为所以又因为所以BOAODOCO（已知）BFAEFOEO（对顶角相等）FODEOC所以FODEOC所以FDEC直接证明证（分析法）要证明CE=DF，只需证明为此只需证明FODEOCFOEOFODEOCDOCO为了证明只需为了证明只需证明也只需DOCOBDOACOFOEO）（因为已知BFAEBOAO（已知）BDOACO因为是对顶角，所以它们相等，从而FODEOC与FODEOC成立，因此命题成立.分析法解题方向比较明确，利于寻找解题思路；综合法条理清晰，易于表述。通常以分析法寻求思路，再用综合法有条理地表述解题过程直接证明（练习）.221,0,0.1abbaba求证：若直接证明（练习）.11,1,1.2abbaba求证：若证要证11abba只需证明112abba只需证明只需证明22)1(abba0)1)(1(22ba11ba1122ba01,0122ba0)1)(1(22ba因此所以原命题成立.直接证明,,abc3.△ABC三边长的倒数成等差数列，求证：.90B证明：acb212)(12cabbcab1acbac222acbcaB2222cos因为a,b,c为△ABC三边所以a+c>b01cab所以cosB>090B因此直接证明（回顾小结）分析法解题方向比较明确，利于寻找解题思路；综合法条理清晰，易于表述。通常以分析法寻求思路，再用综合法有条理地表述解题过程分析法综合法概念