高中数学 第一章第三节(134三角函数的应用)课件 苏教版必修4 课件VIP免费

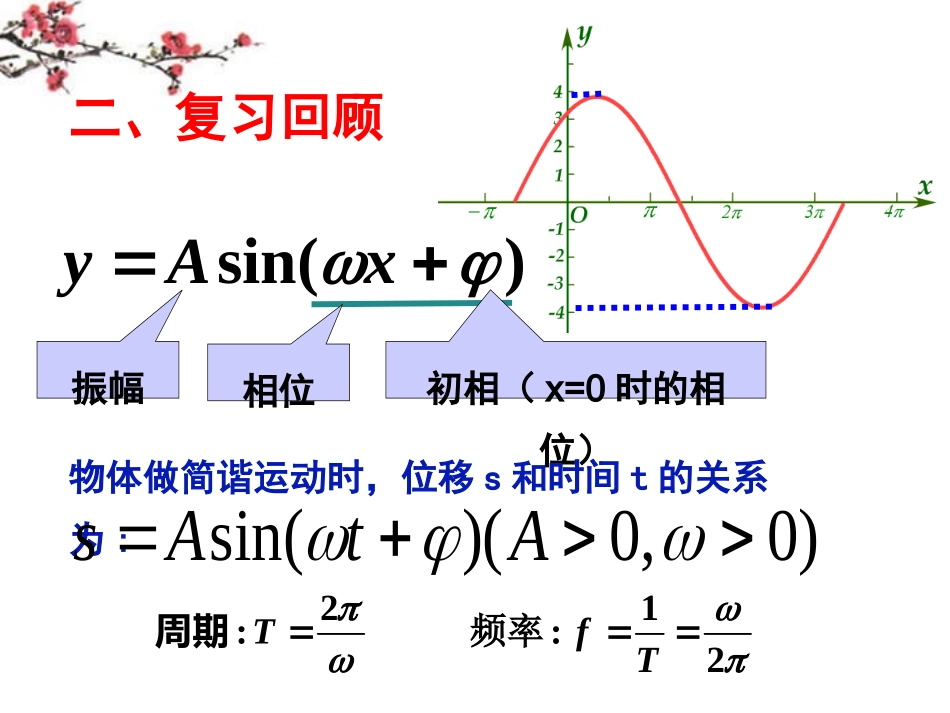
＆1.3.4三角函数的应用(第一课时）一、引入:三角函数能够模拟许多周期现象.因此,在解决问题中有着广泛的应用.本节课我们来研究三角函数的应用问题.)sin(xAy振幅初相（x=0时的相位）相位2:T周期1:2fT频率二、复习回顾物体做简谐运动时，位移s和时间t的关系为:)0,0)(sin(AtAs·O··例1:如图,点O为做简谐运动的物体的平衡位置,取向右的方向为物体位移的正方向,若已知振幅为3㎝,周期为3s,且物体向右运动到距平衡位置最远处时开始计时.(1)求物体对于平衡位置的位移x(㎝)和时间t(s)之间的函数关系.(2)求物体在t=5s时的位置.O三、建构数学解（１）设x和t之间的函数关系为：2π2π则由T==3,可得ω=ω3当t=0时，有x=3sinφ=3,则sinφ=1π又0≤φ〈2π，故可得φ=22ππ2π所以，所求函数关系为x=3sint+=3cost323)20,0)(sin(3tx10π2令t=5,得x=3cos=-1.5,3故该物体在t=5s时的位置是在O点的左侧且距O点1.5cm处。注：本题解法可称为‘待定系数法’引例：如图：一个半径为3m的水轮，水轮圆心o恰在水面上，已知水轮每分钟逆时针转动4圈，如果当水轮上点P从水中浮现时（图中P0)开始计时。(1)将点P距离水面的高度z(m)表示为时间t(s)的函数;(2)点P第一次到达最高点大约要多长时间？p0opA四、探究理解解（1）如图建立平面直角坐标系。由OP在ts内所转过的角为tt152)6024(由OP在ts内所转过的角为tt152)6024(YXOP0PBADP点距离水面的高度即为P点的纵坐标topox152为终边的角为为始边以可知，以t152sin3P点的纵坐标为故tz152sin3（2）点P第一次到达最高点大约要s415思考：点P在D(C、B)点时开始计时，（1）函数的解析式又如何？（2）P点第一次到达最高点分别大约要多少时间?YXOP0PBADCtz152sin3变式1：若水面由于干旱下降了2米，（1）点P距离水面的高度z(m)怎样表示为时间t(s)的函数呢？（2)点P第一次到达最高点大约要多长时间？p0op探究1：如果当水轮上P点从水中浮现时（图中P0点）开始计算时间。op0p23sin()2,(0).152zt2sin,(0)0.73.32Axy1、转动周期变没变？2、ts转过的角度还是不是？t1523、P点的纵坐标还是不是其距离水面的高度？P在元芳，你怎么看？pop0p2)73.0152sin(3tz：故所求函数的关系式为5.5,273.01521)73.0152sin(52)73.0152sin(3ttttz解得取得，令sP5.5要第一次到达最高点约需故变式2：若水面由于降雨上升了2米呢？（1）点P距离水面的高度z(m)怎样表示为时间t(s)的函数呢？（2)点P第一次到达最高点大约要多长时间？p0op五、小憩片刻六、小试牛刀如图，摩天轮的半径为40m，点O距地面的高度为50m，摩天轮做匀速转动，每3min转一圈，摩天轮上点P的起始位置在最低点处。（1）试确定在时刻t(min)时点P距离地面的高度；（2）在摩天轮转动的一圈内，有多长时间点距离地面超过70m？50m40mPO70m如图，某地一天从6时到14时的温度变化曲线近似满足函数sin().yAxb（1）求这一天的最大温差；（2）写出这段曲线的函数解析式.解：（1）观察图象可知，这段时间的最大温差是_______。T/度t/ho6101410203020ºC课后思考作业：)20,0,0(wA（2）从图中可以看出，从6时到14时的图象是函数y=Asin(ωx+φ)+b的半个周期的图象，所以1(3010)10,2A1(3010)20,2b1214682因为点（6，10）是图像的最低点，故所求函数解析式为310sin()20[6,14]84yxx，T/度t/ho61014102030zkk,23268430,432时kk实际问题数学模型实际问题的解抽象概括数学模型的解还原说明推理演算三角应用题的解题策略：数据整理去伪存真八、思想总结