高三数学 第三节 平面向量的数量积与平面向量应用举例复习课件VIP免费

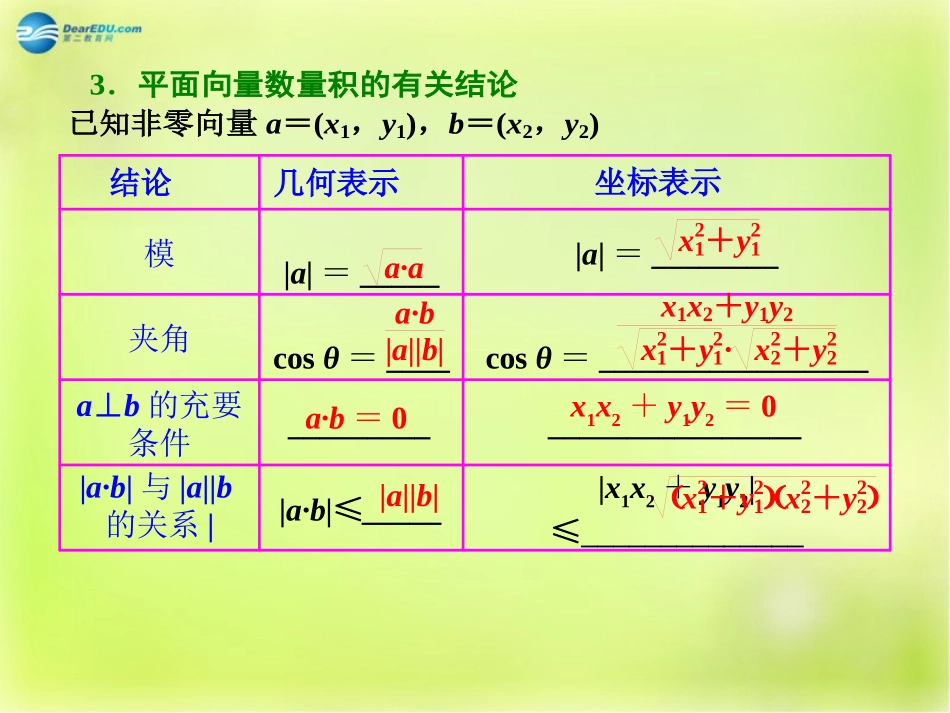
1．平面向量的数量积第三节平面向量的数量积与平面向量应用举例平面向量数量积的定义已知两个向量a和b，它们的夹角为θ，把数量叫做a和b的数量积(或内积)，记作.即a·b＝，规定0·a＝0.非零|a||b|cosθa·b|a||b|cosθ2．向量数量积的运算律(1)a·b＝.b·a(2)(λa)·b＝λ(a·b)＝.a·(λb)(3)(a＋b)·c＝.a·c＋b·c|x1x2＋y1y2|≤______________|a·b|≤_____|a·b|与|a||b的关系|_________________________a⊥b的充要条件cosθ＝_________________cosθ＝____夹角|a|＝________|a|＝_____模结论几何表示坐标表示a·ax21＋y21a·b|a||b|x1x2＋y1y2x21＋y21·x22＋y22a·b＝0x1x2＋y1y2＝0|a||b|x21＋y21x22＋y223．平面向量数量积的有关结论已知非零向量a＝(x1，y1)，b＝(x2，y2)1．(2013·全国卷Ⅱ)已知正方形ABCD的边长为2，E为CD的中点，则AE�·BD�＝________.2解法一：平面向量的基底运算法解法二：平面向量的坐标运算法C3．(2013·南昌模拟)已知向量e1＝cosπ4，sinπ6，e2＝2sinπ4，4cosπ3，则e1·e2＝________.22．(2013·福建高考)在四边形ABCD中，AC�＝(1,2)，BD�＝(－4,2)，则该四边形的面积为()A.5B．25C．5D．104.(2014·沧州模拟)已知平面向量a＝(x1，y1)，b＝(x2，y2)，若|a|＝2，|b|＝3，a·b＝－6.则x1＋y1x2＋y2的值为()A.23B．－23C.56D．－56B5．(2013·福建高考)在四边形ABCD中，AC�＝(1,2)，BD�＝(－4,2)，则该四边形的面积为()A.5B．25C．5D．10解析：依题意得，AC�·BD�＝1×(－4)＋2×2＝0，∴AC�⊥BD�，∴四边形ABCD的面积为12|AC�|·|BD�|＝12×5×20＝5.C平面向量数量积的性质是高考的重点.归纳起来常见的命题角度有：(1)平面向量的模；(2)平面向量的夹角；(3)平面向量的垂直．1．(2013·天津高考)在平行四边形ABCD中，AD＝1，∠BAD＝60°,E为CD的中点．若AC�·BE�＝1,则AB的长为________．12角度一平面向量的模2．(2013·广州调研)已知向量a，b都是单位向量，且a·b＝12，则|2a－b|的值为________．33、(2014·惠州调研)已知向量p＝(2，－3)，q＝(x,6)，且p∥q，则|p＋q|的值为()A.5B.13C．5D．13B利用数量积求解长度问题的处理方法(1)a2＝a·a＝|a|2或|a|＝a·a.(2)|a±b|＝a±b2＝a2±2a·b＋b2.(3)若a＝(x，y)，则|a|＝x2＋y2.[类题通法]2、(2014·云南第一次检测)若平面向量a与平面向量b的夹角等于π3，|a|＝2，|b|＝3，则2a－b与a＋2b的夹角的余弦值等于()A.126B．－126C.112D．－112B1、已知平面向量a，b，|a|＝1，|b|＝3，且|2a＋b|＝7，则向量a与a＋b的夹角为()A.π2B.π3C.π6D．π角度二平面向量的夹角B3、已知向量a，b均为非零向量，(a－2b)⊥a，(b－2a)⊥b，则a，b的夹角为()A.π6B.π3C.2π3D.5π6B1．明确两个结论：(1)两个向量a与b的夹角为锐角，则有a·b>0，反之不成立(因为夹角为0时不成立)；(2)两个向量a与b的夹角为钝角，则有a·b<0，反之不成立(因为夹角为π时不成立)．bababa,cos3）（1、(2013·荆州高中毕业班质量检查Ⅰ)已知向量a与b的夹角是2π3，且|a|＝1，|b|＝4，若(2a＋λb)⊥a，则实数λ＝________.1角度三平面向量的垂直2、在直角三角形ABC中，已知AB�＝(2,3)，AC�＝(1，k)，则k的值为________．－23或113或3±132.3、(2013·山东高考)在平面直角坐标系xOy中，已知OA�＝(－1，t)，OB�＝(2,2)．若∠ABO＝90°，则实数t的值为________．5[典例](2013·江苏高考)已知向量a＝(cosα，sinα)，b＝(cosβ，sinβ)，0<β<α<π.[解](1)证明：由题意得|a－b|2＝2，即(a－b)2＝a2－2a·b＋b2＝2.又因为a2＝b2＝|a|2＝|b|2＝1，所以2－2a·b＝2，即a·b＝0，故a⊥b.(1)若|a－b|＝2，求证：a⊥b；(2)设c＝(0,1)，若a＋b＝c，求α，β的值．注意到|a|=|b|=1是证明的关键！(2)因为a＋b＝(cosα＋cosβ，sinα＋sinβ)＝(0,1)，所以cosα＋cosβ＝0，sinα＋sinβ＝1.由此得，cosα＝cos(π－β)，由0<β<π，得0<π－β<π.又0<α<π，故α＝π－β.代入sinα＋sinβ＝1，得sinα＝sinβ＝12，而α>β，所以α＝5π6，β＝π6.向量相等对应坐标相等是...