高中数学 233 平面与平面垂直的性质课件 新人教版必修2 课件VIP免费

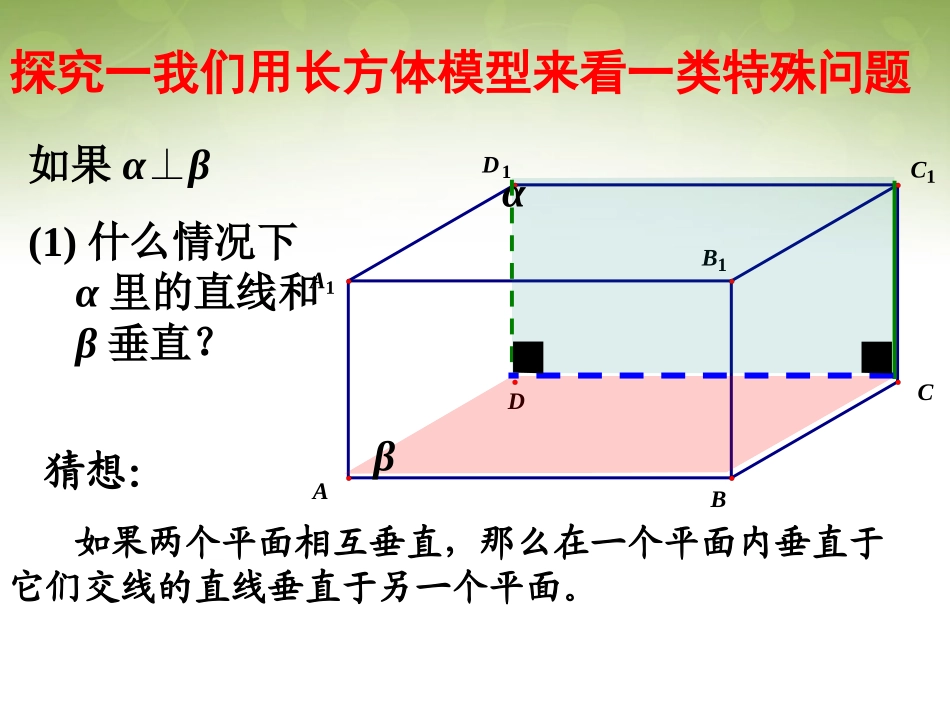
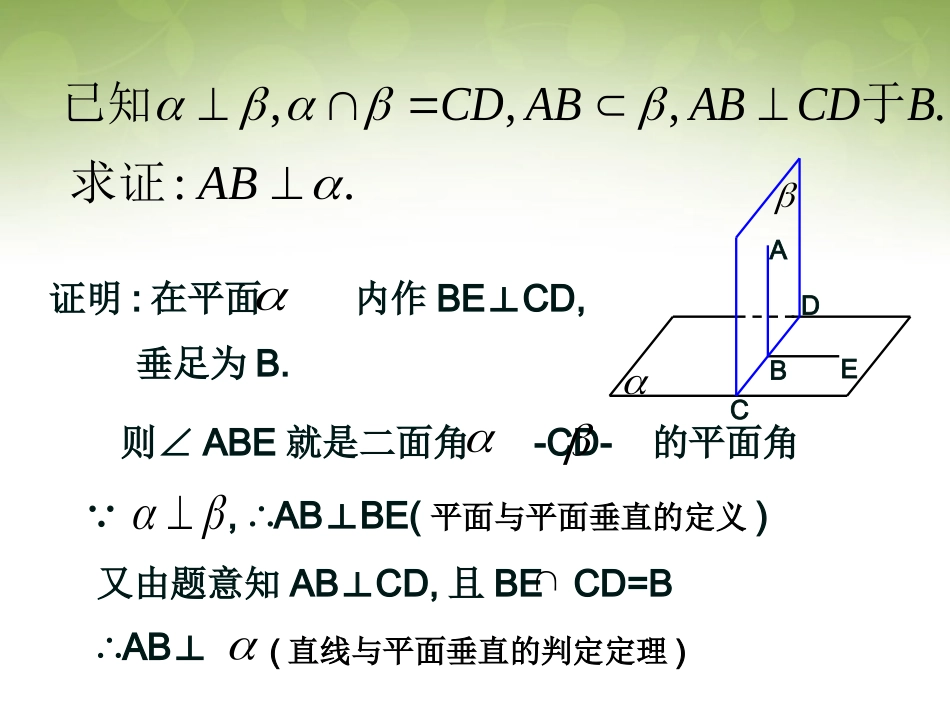
A1D1B1C1CBAD探究一我们用长方体模型来看一类特殊问题αβ如果α⊥β(1)什么情况下α里的直线和β垂直？猜想：如果两个平面相互垂直，那么在一个平面内垂直于它们交线的直线垂直于另一个平面。.,,,BCDABABCD于已知.:AB求证则∠ABE就是二面角-CD-的平面角∵,ABBE(∴⊥平面与平面垂直的定义)又由题意知ABCD,⊥且BECD=BE证明:在平面内作BECD,⊥垂足为B.∴AB⊥(直线与平面垂直的判定定理)DCABbbβαPa思考：设平面⊥平面，点P在平面内，过点P作平面的垂线a，直线a与平面具有什么位置关系?βαPa直线a在平面内已知αβ⊥，Pα∈，Pa,aβ.∈⊥求证：aα.∩证明：设α∩β=c，过点P在平面α内作直线b⊥c，则由性质定理得bβ.⊥因为经过一点只能有一条直线与平面β垂直，所以直线a应与b直线重合.所以aα.∩βαbPac如果两个平面垂直，那么经过第一个平面的一点垂直于第二个平面的直线，在第一个平面内．例4,,,aaa判断与位置关系解：设bαβall在α内作直线b⊥llbblba又//abba//a如果两个平面垂直，则在一个平面内垂直于它们的交线的直线垂直于另一个平面.三、两个平面垂直的性质定理:为作辅助线提供了理论依据αβαβmlβlαlm如果两个平面垂直，那么经过第一个平面的一点垂直于第二个平面的直线，在第一个平面内．为判定直线在平面内提供了理论依据αllAαAβlβα