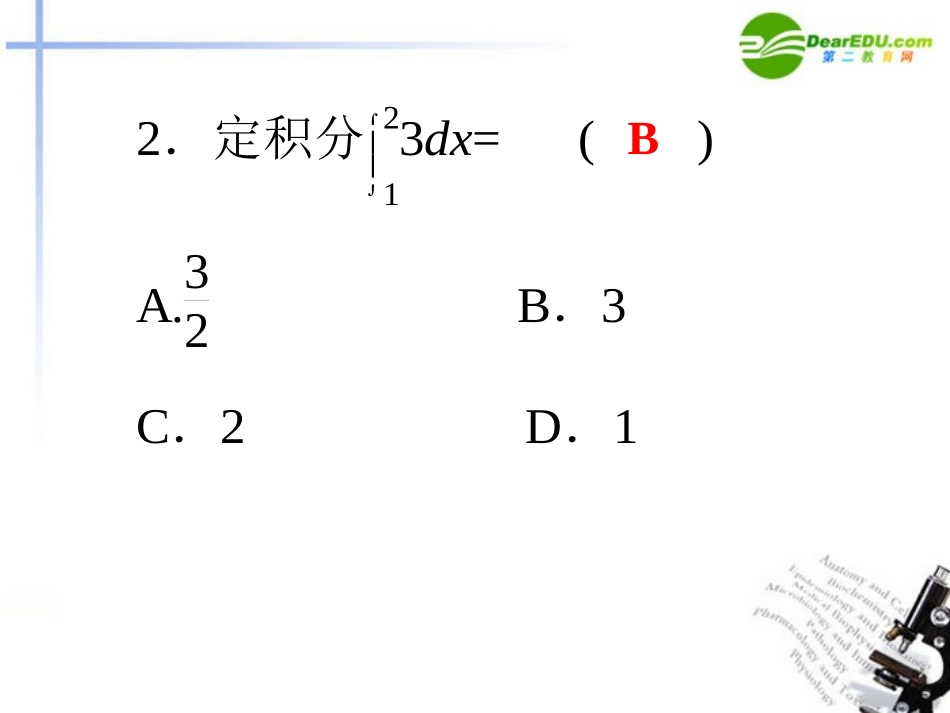
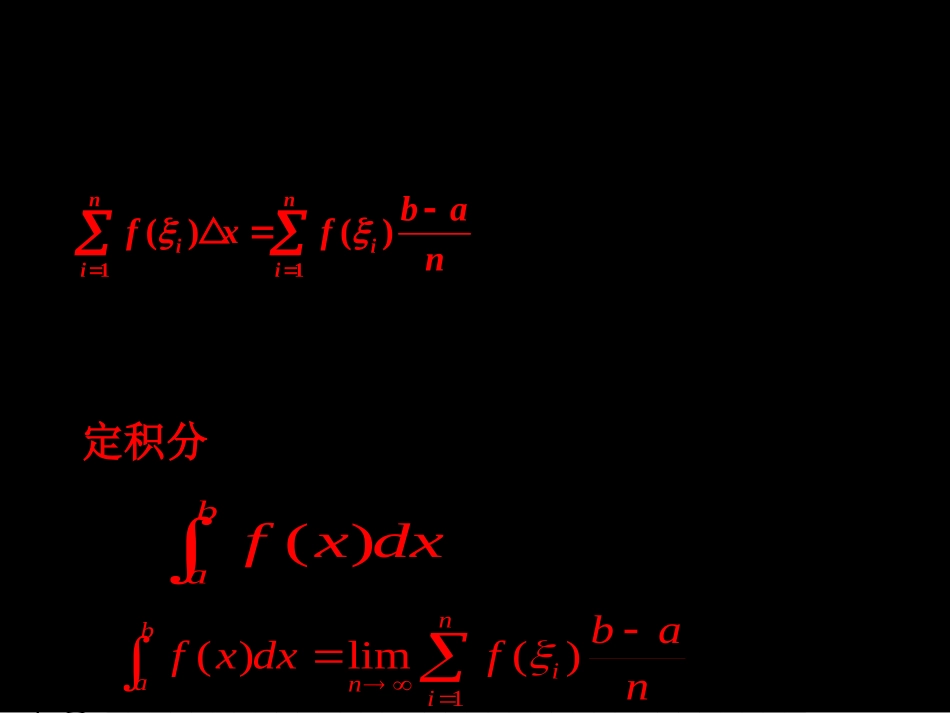1.5.41.5.4定积分的概定积分的概念念1.如果函数f(x)在区间[a,b]上连续,用分点将区间[a,b]等分成n个小区间,在每个小区间上任取一点ξi(i=1,2,…,n),作和式①_____________,当n→∞时,上述和式无限接近于某个常数,这个常数叫做函数f(x)在区间[a,b]上的②________,记作③________,即④_________________________________.11()()nniiiibafxfn定积分()bafxdx1()lim()nbianibafxdxfn2.定积分123dx=()A.32B.3C.2D.1B4.∫2π0cosxdx=________.•答案:0解析:如下图所示,∫2π0cosxdx=B1-B2+B3=0.05.已知ab[f(x)+g(x)]dx=12,abg(x)dx=6,求ab3f(x)dx.解:∵abf(x)dx+abg(x)dx=ab[f(x)+g(x)]dx,∴abf(x)dx=12-6=6.∴ab3f(x)dx=3abf(x)dx=3×6=18.[解]令f(x)=3x+2.(1)分割在区间[1,2]上等间隔地插入n-1个分点,把区间[1,2]等分成n个小区间[n+i-1n,n+in](i=1,2,…,n)每个小区间的长度为Δx=n+in-n+i-1n=1n例1利用定积分定义,计算12(3x+2)dx的值.例1:利用定积分的定义,计算的值.130xdx[解]令f(x)=x3.在区间[0,1]上等间隔地插入n-1个分点,把区间[1,2]等分成n个小区间[(i-1)/n,i/n](i=1,2,…,n)取则1333401122411,lim()lim1(1)111limlim(1)244nninniinniixdxinnnnnnnn作业:P50A组:5(1)B组:3