高中数学 绝对值不等式的解法课件 新人教A版选修4-5 课件VIP免费

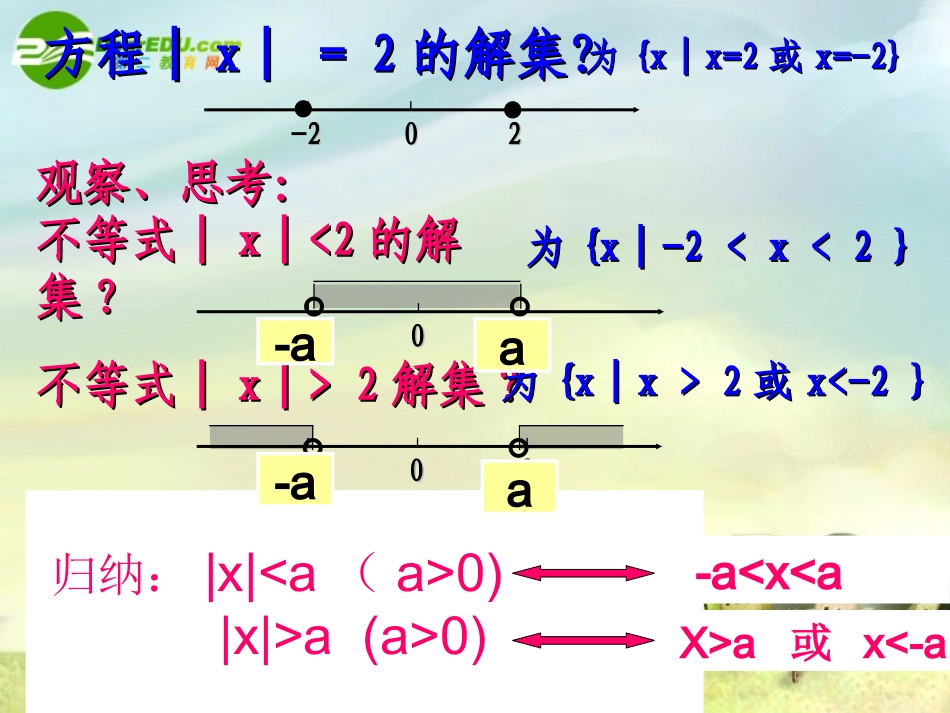
绝对值不等式的解法绝对值不等式的解法复习：X=0|x|=X>0x0X<0-x1.绝对值的定义:2.几何意义:Ax1XOBx2|x1||x2|=|OA|=|OB|一个数的绝对值表示这个数对应的点到原点的距离.类比：|x|<3的解|x|>3的解观察、思考：观察、思考：不等式│不等式│x│<2x│<2的解的解集集??方程│方程│x│x│＝＝22的解集？的解集？为为{x│x=2{x│x=2或或x=-2}x=-2}0022-2-2为为{x│-22x│>2解集解集??为为{x│x>2{x│x>2或或x<-2}x<-2}0022-2-20022-2-2|x|<-2的解|x|>-2的解归纳：|x|0)|x|>a(a>0)-aa或x<-a-aa-aa如果a＞0，则axaxax或axaax如果把|x|<2中的x换成“x-1”,也就是|x-1|<2如何解？引伸：解题反思：如果把|x|>2中的x换成“3x-1”,也就是|3x-1|>2如何解？整体换元。归纳：型如|f(x)|a(a>0)不等式的解法:()()fxaafxa()()fxafxaa或f(x)例1解不等式532x解：这个不等式等价于5325x3533235x822x41x因此，不等式的解集是（–1，4）例2解不等式32x＞5解：这个不等式等价于或（1）（2）532x（1）的解集是（4，+∞），（2）的解集是（－∞，－1），∴原不等式的解集是（4，+∞）∪（－∞，－1）。532x巩固练习：求下列不等式的解集①|2x+1|<5②3|1-4x|>9③|4x|<-1④|x2-5x|>-6⑤3<|2x+1|<5（-3，2）（-∞，-1/2）∪（1，+∞）R（-3，-2）∪（1，2）例:解不等式|5x-6|<6–x引伸：型如|f(x)|a的不等式中“a”用代数式替换，如何解？解：对绝对值里面的代数式符号讨论：5x-6≥05x-6<6-x()Ⅰ或()Ⅱ5x-6<0-（5x-6）<6-x解()Ⅰ得：6/5≤x<2解()Ⅱ得：00所以00时,转化为-(6-x)<5x-6<(6-x)由绝对值的意义，原不等式转化为：6-x>0-(6-x)<5x-6<(6-x)综合得00时,转化为-(6-x)<5x-6<(6-x)由绝对值的意义，原不等式转化为：6-x>0-(6-x)<5x-6<(6-x)X<6-(6-x)<5x-65x-6<(6-x)00是否可以去掉有更一般的结论：|f(x)|g(x)f(x)>g(x)或f(x)<-g(x)类型1练习：把下列绝对值不等式转化为同解的非绝对值不等式。3、|x-1|>2(x-3)4、2xx2xx5、|2x+1|>|x+2|1、|2x-3|<5x2、|x2-3x-4|>4类型2xaxbcxaxbc和125xx例：方法1：几何意义方法2：去绝对值方法3：函数的观点解不等式237xx24337xx课堂小结：(1)数学知识:常见的绝对值不等式的解法(2)数学思想分类讨论的思想整体的思想转化的思想同学们再见！引例：某电机厂承担一项任务，为自来水厂加工一种圆形管道，管道直径设计为50毫米，由于实际加工过程中存在误差，规定成品管道实际直径与设计值相差不能超过1毫米，否则为次品，设成品管道的实际半径x毫米，那么x应该满足什么条件？解：由题意成品管道的直径为2x毫米由绝对值的意义可知，结果也可表示为:|2x-50|≦1050解不等式：|x-1|>|x-3|方法一方法二方法三反思评价我们的解题方法：解：因为|x-1|>|x-3|所以两边平方可以等价转化为（x-1)2>(x-3)2化简整理：x>2平方法：注意两边都为非负数|a|>|b|依据：a2>b2解：如图，设“1”对A，“3”对应B，“X”对应M（不确定的），即为动点。|x-1|>|3-x|由绝对值的几何意义可知：|x-1|=MA|x-3|=MB0132AB几何的意义为MA>MB,分类讨论：分析：两个|x-1|、|x-3|要讨论，按照绝对值里面的代数式符号进行讨论。可以借助数轴分类。解:使|x-1|=0,|x-3|=0，未知数x的值为1和30131、当x3≧时，原不等式可以去绝对值符号化为：x-1>x-3解集为R，与前提取交集，所以x3≧；2、当1x<3≦时,同样的方法可以解得22