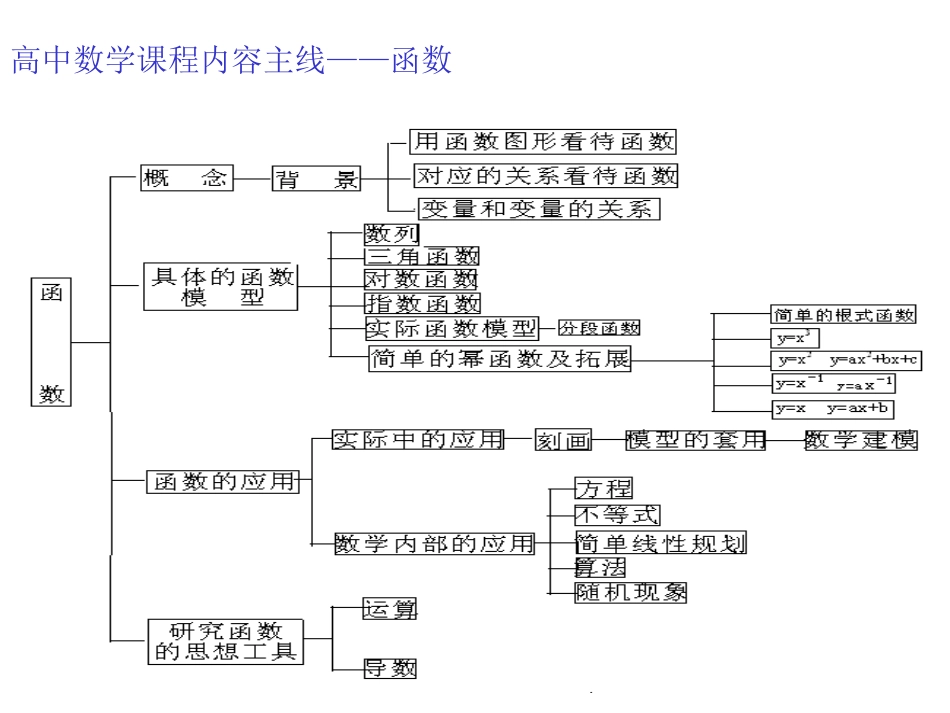
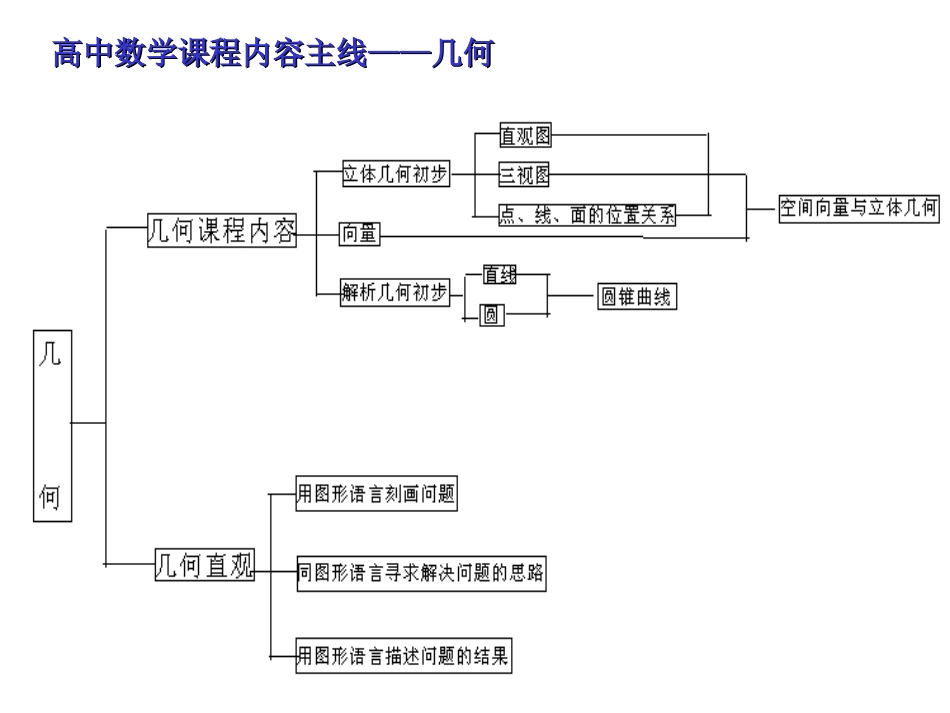
高中数学课程的内容主线函数函数几何几何运算运算算法算法统计概率统计概率应应用用高三知识复习高三知识复习::高中数学课程内容主线——函数高中数学课程内容主线——几何高中数学课程内容主线——几何高中数学课程内容主线——运算高中数学课程内容主线——运算高中数学课程内容主线——算法高中数学课程内容主线——统计概率高中数学课程内容主线——统计概率高中数学课程内容主线——应用高中数学课程内容主线——应用必修必修55个模块个模块必修与选修Ⅰ必修与选修Ⅰ((文科文科))必修与选修Ⅱ必修与选修Ⅱ((理科理科))不等式选讲坐标系与参数方程矩阵与变换高中数学存在知识结构知识之间有联系知识运用要方法知识调用需思想教材教学要求1.教学目标决定高考指导思想(高考指导思想在新教材实验开始时已定位)2.教学内容决定高考内容(支持新知识的落实,保持传统知识考查,必考与选考)3.知识地位决定考查重点并涉及考查形式(做为基础知识的知识,做为基础知识又具有方法功能的知识)基础知识复数、解几(两章)、立几、概率统计等既是基础又是工具的知识集合、函数、向量、不等式、导数等知识特点:教材教学要求的提示:教材教学要求的提示:1.重新构建知识结构;2.培养提升思想方法;3.研究新增知识考法.横向联系(1)教学中分散,复习中重组.三角:三角函数,三角简单变换与变形;解三角形;数列:两类基础数列,数学归纳法;函数:一次、二次、对、指、幂函数,三角函数,数列,函数两域四性,导数;不等式:不等式,线性规划,导数;概率与统计:必修、选修。运算:字母,数(指、对;复数),向量,三角;重新构建知识结构:横向联系(2)教学中内涵,复习中体现.基础石:集合、命题、量词、条件、逻辑(数学语言与本质属性)函数链(代数):函数,不等式,三角函数,数列,导数,函数思想应用(解几,立几,向量)向量链(几何):向量,数列,复数,函数,三角,立几,解几几何图(数形结合):函数,三角,数列,不等式,立几,解几,复数,导数、积分,概率,统计重新构建知识结构:例1例2例4已知事件A与B是互斥事件,事件C与B是对立事件,且P(B)=,求P(A).BCA思考:{an}表达式未知的条件下,如何证、判?•例5.设函数f(x)与数列{an}满足关系:(1)a1>α,其中α是方程f(x)=x的实根;(2)an+1=f(an),n∈N*.如果f(x)的导数满足0α(n∈N*);(Ⅱ)判断an与an+1的大小,并证明你的结论。(Ⅰ)证明:(数学归纳法)当n=1时,由题设知a1>α成立;假设当n=k时,ak>α成立, fˊ(x)>0,∴f(x)为增函数,ak+1=f(ak)>f(α)=α,于是ak+1>α,即对于n=k+1也成立,综合上述得,对n∈N*,都有an>α成立.(Ⅱ)解:令g(x)=x–f(x),则gˊ(x)=1–fˊ(x)>0,故g(x)为增函数,由g(α)=α–f(α)=0,得g(x)>g(α)=0,即x>f(x),由(Ⅰ)知,an>α,∴an>f(an)=an+1.(n∈N*)一看可知:a·b是实数,是x的函数!•例6.已知向量a=(x,x–4),向量b=(x2,x),x[–4,2].(1)试用x表示a·b;(2)求a·b的最大值,并求此时a、b夹角的大小。构建知识结构:2)(适当)纵向深化(复盖)揭示本质解法彻底解决问题例8.研究性课题:正方体与内接正四面体如图,A1C是一个平行六面体.请连接AB,AC,AD,BC,BD,CD,看得出一个什么几何体.称四面体ABCD为平行六面体A1C的内接四面体;平行六面体A1C为四面体ABCD的外接平行六面体.任何一个平行六面体都存在内接四面体,当然,任何一个四面体都存在外接平行六面体.由此看来,平行六面体与四面体有着十分紧密的联系.请进行一些探索,看看能得出些什么结论?△培养提升方法思想:1.教学中浅现,复习中深化数学方法的应用(结合数学知识复习,结合解决数学问题,应用于解决实际问题)。高考将仍然“坚持多角度,多层次考查”的命题思路。这要求学生完全掌握换元法、待定系数法、定义法、分析法、反证法、数学归纳法、构造法。培养提升方法思想:2.教学中存在,复习中凸现数感与猜想(直觉思维);推理与计算(逻辑思维)。高考涉及的主要数学思想:函数与方程的思想;数形结合的思想;分类讨论的思想;化归与转化的思想。同时也涉及:归纳、猜想、论证的思想方法;运动与变化的思想方法;特殊与...