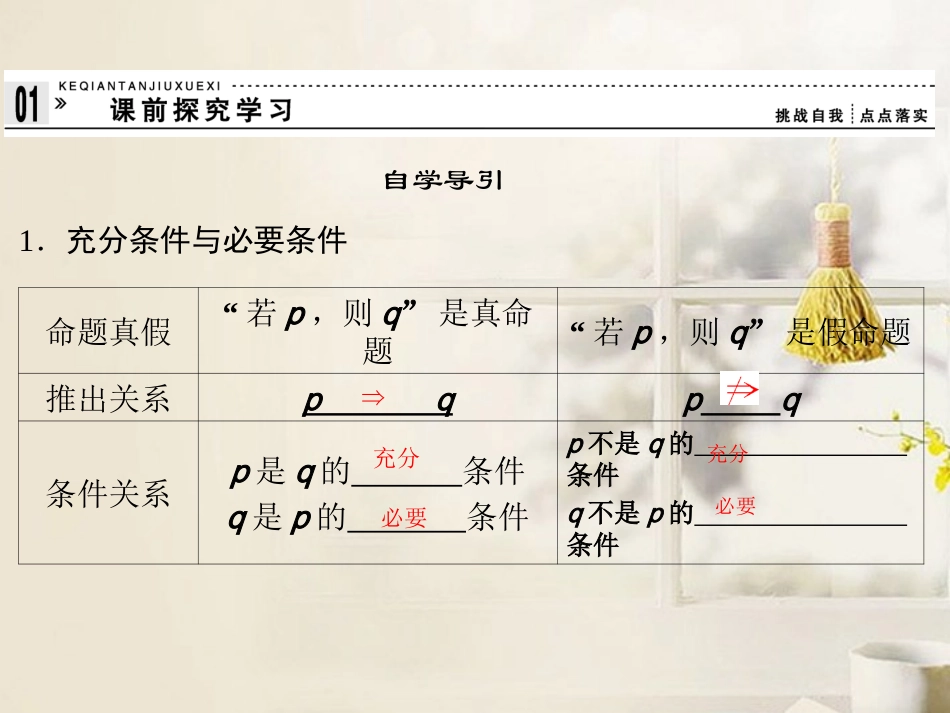
1.2充分条件与必要条件1.2.1充分条件与必要条件1.2.2充要条件【课标要求】1.理解充分条件、必要条件、充要条件的意义.2.会求(判定)某些简单命题的条件关系.【核心扫描】1.判断充分条件、必要条件、充要条件.(重点)2.证明充要条件和求充要条件.(难点)自学导引1.充分条件与必要条件命题真假“若p,则q”是真命题“若p,则q”是假命题推出关系pqpq条件关系p是q的条件q是p的条件p不是q的条件q不是p的条件⇒充分必要充分必要试一试:在逻辑推理中p⇒q,能否表达成以下5种说法:①“若p,则q”为真命题;②p是q的充分条件;③q是p的必要条件;④q的充分条件是p;⑤p的必要条件是q.提示可以.这五种说法表示的逻辑关系是一样的,都能表示p⇒q,只是说法不同而已.2.充要条件的概念一般地,如果既有p⇒q,又有q⇒p,就记作p⇔q,此时,我们说p是q的充分必要条件,简称.显然,如果p是q的充要条件,那么q也是p的,即如果p⇔q,那么p与q互为充要条件.想一想:p是q的充要条件与p的充要条件是q有什么区别?提示p是q的充要条件指的是p⇒q是充分性,q⇒p是必要性,即p是条件,q是结论;p的充要条件是q中,q⇒p是充分性,p⇒q是必要性,即q是条件,p是结论.充要条件充要条件名师点睛1.充分条件、必要条件、充要条件的判断(1)定义法若p⇒q,但qp,则p是q的充分而不必要条件;若q⇒p,但pq,则p是q的必要而不充分条件;若p⇒q且q⇒p,则p是q的充要条件;若pq且qp,则p是q的既不充分也不必要条件.(2)集合法首先建立与p,q相应的集合,即p:A={x|p(x)};q:B={x|q(x)}.若A⊆B,则p是q的充分条件;若B⊆A,则p是q的必要条件;若AB,则p是q的充分而不必要条件;若BA,则p是q的必要而不充分条件;若A=B,则p是q的充要条件;若AB,BA,则p是q的既不充分也不必要条件.(3)传递性法由于逻辑联结符号“⇒”“⇐”“⇔”具有传递性,因此可根据几个条件的关系,经过若干次的传递,判断所给的两个条件之间的相互关系.(4)等价命题法当某一命题不易直接判断条件与结论的充要关系(特别是对于否定形式或“≠”形式的命题)时,可利用原命题与其逆否命题的等价性来解决,即等价转化为判断其逆否命题.2.应用充分条件、必要条件、充要条件时需注意的问题(1)确定条件是什么,结论是什么;(2)尝试从条件推结论,从结论推条件;(3)确定条件是结论的什么条件;(4)要证明命题的条件是充要的,就是既要证明原命题成立,又要证明它的逆命题成立.证明原命题即证明条件的充分性,证明逆命题即证明条件的必要性.[思路探索]解答本题首先判断是否有p⇒q和q⇒p,再根据定义下结论,也可用等价命题判断.解(1)在△ABC中,显然有∠A>∠B⇔BC>AC,所以p是q的充要条件.(2)因为:x=2且y=6⇒x+y=8,即綈q⇒綈p,但綈p綈q,所以p是q的充分不必要条件.【变式1】指出下列各组命题中,p是q的什么条件(在“充分不必要条件,必要不充分条件,充要条件,既不充分也不必要条件”中选一种作答)?(1)p:△ABC中,b2>a2+c2,q:△ABC为钝角三角形;(2)p:△ABC有两个角相等,q:△ABC是正三角形;(3)若a,b∈R,p:a2+b2=0,q:a=b=0.解(1)△ABC中, b2>a2+c2,∴cosB=a2+c2-b22ac<0,∴B为钝角,即△ABC为钝角三角形,反之若△ABC为钝角三角形,B可能为锐角,这时b2
0恒成立的充要条件是a>1.证明当a=0时,2x+1>0不恒成立;当...