高中数学：221向量加法运算及其几何意义课件人教版必修4 课件VIP免费

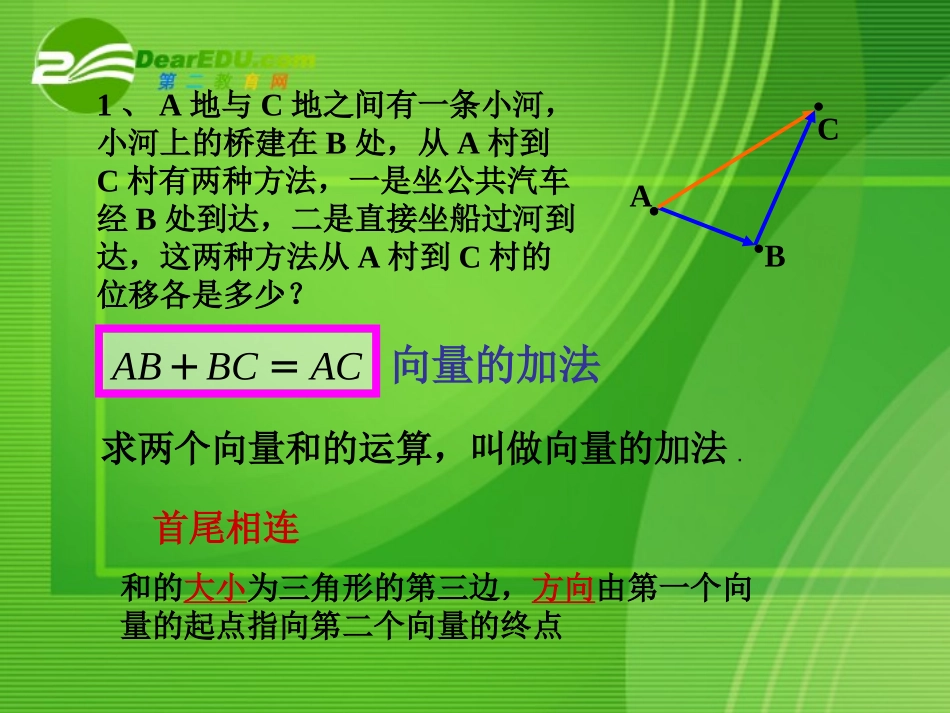
2.2.1向量加法运算及其几何意义回顾1.向量：有向线段：2.向量的模：4.零向量：3.平行向量：4.相等向量：既有大小，又有方向的量，带有方向的线段（起点、方向、长度）向量的长度（表示为）长度为0的向量方向相同或相反的非零向量长度相等且方向相同的向量平行向量即为共线向量aABC1、A地与C地之间有一条小河，小河上的桥建在B处，从A村到C村有两种方法，一是坐公共汽车经B处到达，二是直接坐船过河到达，这两种方法从A村到C村的位移各是多少？ABBCAC+=�首尾相连和的大小为三角形的第三边，方向由第一个向量的起点指向第二个向量的终点求两个向量和的运算，叫做向量的加法.向量的加法bA·CBabab问题:已知，求作向量+,向量加法的三角形法则aabababABBCAC��+=+=要点：两向量首尾相连,abab2,当向量是共线向量时,又如何作出来练习：,;;ababba1,如图,已知,求作①②++ab(1)ab(2)abo·ABb+ab�a||||||abab++<,ab（1）当不共线时||||||abab一般地，有+£+不难发现，,ab（2）当不共线时b,;;ababba1,如图,已知,求作①②++abaabab+ba+ab力的合成ABC向量加法的平行四边形法则两向量有公共起点和的大小为平行四边形的从同一个起点出发的对角线，方向由公共起点指向平行四边形的对角O练习：3、长江两岸之间没有大桥的地方，常常通过轮渡进行运输。如图所示，一艘船从长江南岸A点出发，以5km/h的速度向垂直于对岸的方向行驶，同时江水的速度为向东2km/h。（1）试用向量表示江水速度、船速以及船实际航行的速度。（2）求船实际航行的速度的大小与方向。ACDB数的加法满足交换律与结合律，即对任意a，bR∈a+b=b+a(a+b)+c=a+(b+a)任意向量的加法是否也满足与？、ab+=+abba)++=++(ab)ca(bc0______;(2)0______aa练习5,(1)aa任意向量与零向量的和仍为零向量84P6、课本3、4)+=+++=++abba(ab)ca(bc作业：84P课本２9P１课本１，２，３